
分析 (1)利用对数的真数大于0,列出不等式,利用绝对值不等式的解法求解函数的定义域即可.
(2)利用函数的定义域为R,通过绝对值的几何意义,转化求解即可.
解答 解:(1)当a=3时,|x-2|+|x+3|-9>0,当x<-3时,不等式化为:-2x-10>0,解得x<-5,
当x>2时,不等式化为2x-8>0解得x>4,
当-3≤x≤2时,不等式无解,
所以函数的定义域为:(-∞,-5)∪(4,+∞)…(5分)
(2)由题意|x-2|+|x+a|>9恒成立
∵|x-2|+|x+a|≥|x-2-x-a=|a+2|,
∴|a+2|>9.
解得a>7或a<-11.…(10分)
点评 本题考查函数的定义域,函数恒成立以及绝对值不等式的解法,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{10}}{5}$ | B. | $\frac{7\sqrt{10}}{5}$ | C. | $\frac{8\sqrt{10}}{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
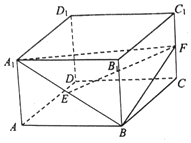 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{π}{8}$ | B. | $\frac{{2π-3\sqrt{3}}}{4}$ | C. | $\frac{{π-\sqrt{2}}}{2}$ | D. | $\frac{{π-\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
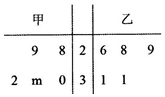 为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )
为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(位:℃)制成如图所示的茎叶图,已知甲地该月11时的平均气温比乙地该月11时的平均气温高1℃,则甲地该月11时的平均气温的标准差为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com