练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
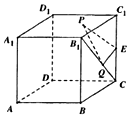
    4．如右图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E为棱CC1的中点，点P，Q分别为面A1B1C1D1和线段B1C上的动点，则△PEQ周长的最小值为$\sqrt{10}$．

    分析 由题意，△PEQ周长取得最小值时，P在B1C1上，在平面B1C1CB上，设E关于B1C的对称点为N，关于B1C1的对称点为M，求出MN，即可得出结论．

    解答 解：由题意，△PEQ周长取得最小值时，P在B1C1上，
    在平面B1C1CB上，设E关于B1C的对称点为N，关于B1C1的对称点为M，则
    EM=2．EN=$\sqrt{2}$，∠MEN=135°，
    ∴MN=$\sqrt{4+2-2×2×\sqrt{2}×（-\frac{\sqrt{2}}{2}）}$=$\sqrt{10}$．
    故答案为$\sqrt{10}$．

    点评 本题考查棱柱的结构特征，考查对称点的运用，考查余弦定理，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．已知数列{an}的前n项和为Sn，若a1=1，a2n=n-an，a2n+1=an+1，则S100=1306．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=ex+（a+1）x（其中e为自然对数的底数）
    （1）设过点（0，0）的直线l与曲线f（x）相切于点（x0，f（x0）），求x0的值；
    （2）若函数g（x）=ax2+ex+1的图象与函数f（x）的图象在（0，1）内有交点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：
    测试指标[85，90）[90，95）[95，100）[100，105）[105，110）
    机床甲81240328
    机床乙71840296
    （1）试分别估计甲机床、乙机床生产的零件为优品的概率；
    （2）甲机床生产一件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元；假设甲机床某天生产50件零件，请估计甲机床该天的日利润（单位：元）；
    （3）从甲、乙机床生产的零件指标在[90，95）内的零件中，采用分层抽样的方法抽取5件，从这5件中任选2件进行质量分析，求这2件都是乙机床生产的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．函数f（x）=2sin（3x+φ）的图象向右平移动$\frac{π}{12}$个单位，得到的图象关于y轴对称，则|φ|的最小值为（　　）
    A．$\frac{π}{12}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{5π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知双曲线$M：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1、F2，|F1F2|=2c．若双曲线M的右支上存在点P，使$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$，则双曲线M的离心率的取值范围为（　　）
    A．$（1，\frac{{2+\sqrt{7}}}{3}）$B．$（1，\frac{{2+\sqrt{7}}}{3}]$C．（1，2）D．（1，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．倾斜角为$\frac{π}{3}$的直线l过抛物线y2=ax（a＞0）的焦点F，且与抛物线交于点A、B，l交抛物线的准线于点C（B在A、C之间），若$|{BC}|=\frac{8}{3}$，则a=（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在平面四边形ABCD中，$AB⊥BC，AB=2，BD=\sqrt{5}，∠BCD=2∠ABD，△ABD$的面积为2．
    （1）求AD的长；
    （2）求△CBD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．现阶段全国多地空气质量指数“爆表”．为探究车流量与PM2.5浓度是否相关，现对北方某中心城市的车流量最大的地区进行检测，现采集到12月某天7个不同时段车流量与PM2.5浓度的数据，如下表：
    车流量x（万辆/小时）1234567
    PM2.5浓度y（微克/立方米）30363840424450
    （1）根据上表中的数据，用最小二乘法求出y关于x的线性回归方程；
    （2）规定当PM2.5浓度平均值在（0，50]，空气质量等级为优；当PM2.5浓度平均值在（50，100]，空气质量等级为良；为使该城市空气质量为优和良，利用该回归方程，预测要将车流量控制在每小时多少万辆内（结果以万辆做单位，保留整数）．
    附：回归直线方程：$\widehaty=\widehatbx+\widehata$，其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata=\overline y=\widehatb\overline x$．

    查看答案和解析>>

    同步练习册答案