【题目】中央电视台电视公开课《开讲了》需要现场观众，先邀请甲、乙、丙、丁四所大学的40名学生参加，各大学邀请的学生如下表所示：
大学 | 甲 | 乙 | 丙 | 丁 |
人数 | 8 | 12 | 8 | 12 |
从这40名学生中按分层抽样的方式抽取10名学生在第一排发言席就座．
（1）求各大学抽取的人数；
（2）从（1）中抽取的乙大学和丁大学的学生中随机选出2名学生发言，求这2名学生来自同一所大学的概率．
科目：高中数学 来源： 题型：
【题目】已知甲、乙两地相距为
千米，汽车从甲地匀速行驶到乙地，速度每小时不超过
千米.已知汽车每小时的运输成本（单位：元）由可变部分和固定部分组成：固定部分为
元，可变部分与速度
（单位; 
）的平方成正比，且比例系数为
.
（1）求汽车全程的运输成本
（单位：元）关于速度
（单位; 
）的函数解析式；
（2）为了全程的运输成本最小，汽车应该以多大的速度行驶？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点，焦点在
轴上的椭圆，离心率为
且过点
，过定点
的动直线与该椭圆相交于
两点．
（1）若线段
中点的横坐标是
，求直线
的方程；
（2）在
轴上是否存在点
，使
为常数？若存在，求出点
的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在多面体
中，四边形
为正方形，
，
，
，
，
，
为
的中点．
（1）求证：
平面；
（2）在线段
上是否存在一点
，使得二面角
的大小为
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】第
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行，为了解我校学生“收看奥运会足球赛”是否与性別有关，从全校学生中随机抽取
名进行了问卷调查，得到
列联表，从这名同学中随机抽取
人，抽到“收看奥运会足球赛 ”的学生的概率是
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
（1）请将上面的列联表补充完整，并据此资料分析“收看奥运会足球赛”与性別是否有关；
（2）若从这名同学中的男同学中随机抽取
人参加有奖竞猜活动，记抽到收看奥运会足球赛”的学生人数为
，求
的分布列和数学期望.
参考公式：
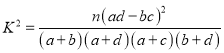，其中
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
是数列
的前
项和，且满足
，等差数列
的前
项和为
,且
， 
.
（Ⅰ）求数列
与
的通项公式；
（Ⅱ）若数列
的通项公式为
，问是否存在互不相等的正整数
， 
， 
使得
， 
， 
成等差数列，且
， 
， 
成等比数列？若存在，求出
， 
， 
；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当函数
在点
处的切线方程为
，求函数的解析式；
（2）在（1）的条件下，若
是函数的零点，且
，求
的值；
（3）当
时，函数有两个零点
，且
，求证：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在边长为1的等边三角形
中，
分别是
，
上的点，
，
是
的中点，
与
交于点
，
沿折起，得到如图2所示的三棱锥
，其中
.
（1）求证：平面
平面
（2）若为，上的中点，
为中点，求异面直线与
所成角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
