
【题目】已知函数f(x)=x2﹣x+c(c∈R)的一个零点为1. (Ⅰ)求函数f(x)的最小值;
(Ⅱ)设 ![]() ,若g(t)=2,求实数t的值.
,若g(t)=2,求实数t的值.
【答案】解:(Ⅰ)∵函数f(x)=x2﹣x+c的一个零点为1, ∴f(1)=0,即12﹣1+c=0,解得c=0,
∴ ![]() ,
,
∴当 ![]() 时,函数f(x)的最小值为-
时,函数f(x)的最小值为- ![]() .
.
(Ⅱ) 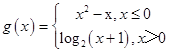 ,
,
∵g(t)=2,
∴当t≤0时,g(t)=t2﹣t=2,解得t=﹣1,或t=2(舍去);
当t>0时,g(t)=log2(t+1)=2,解得t=3.
综上所述,实数t的值为﹣1或3.
【解析】(Ⅰ)由已知可得f(1)=0,易求c,配方后利用二次函数的性质可求最小值;(Ⅱ)分t≤0,t>0两种情况讨论,表示出方程g(t)=2可解t值;
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
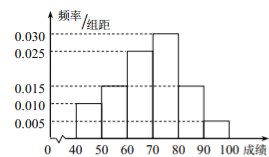
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
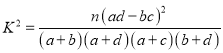 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是 ![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中又放回的摸球,每次摸出一个,共摸5次 ①恰好有3次摸到红球的概率;
②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是 ![]() ,求p的值.
,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)﹣g(x)极值点的情况是( ) 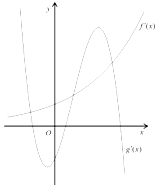
A.只有三个极大值点,无极小值点
B.有两个极大值点,一个极小值点
C.有一个极大值点,两个极小值点
D.无极大值点,只有三个极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1+an= ![]() ﹣
﹣ ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求a2 , a3 , a4;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c.
(1)若a=2 ![]() ,A=
,A= ![]() ,且△ABC的面积S=2
,且△ABC的面积S=2 ![]() ,求b,c的值;
,求b,c的值;
(2)若sin(C﹣B)=sin2B﹣sinA,试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com