Question

11．在同一直角坐标系中，画出函数y=sinx，x∈[0，2π]；y=cosx，x∈[-$\frac{π}{2}$，$\frac{3π}{2}$]的图象，通过观察两条曲线，说出它们的异同．

Answer 1

分析 在同一直角坐标系中，画出函数y=sinx，x∈[0，2π]；y=cosx，x∈[-$\frac{π}{2}$，$\frac{3π}{2}$]的图象，数形结合可得结论．

解答 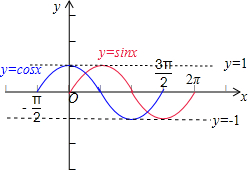解：在同一直角坐标系中，
画出函数y=sinx，x∈[0，2π]以及
y=cosx，x∈[-$\frac{π}{2}$，$\frac{3π}{2}$]的图象，
如图所示：
它们的形状是相同的，只是它们在坐标系中的位置不同，
把函数y=sinx，x∈[0，2π]的图象向左平移$\frac{π}{2}$个单位，
即可得到y=cosx，x∈[-$\frac{π}{2}$，$\frac{3π}{2}$]的图象．

点评 本题主要考查正弦函数、余弦函数的图象，以及它们之间的区别，属于基础题．