Question

15．飞机沿水平方向飞行，在A处测得正前下方地面目标C的俯角为30°，向前飞行10000米到达B处，此时测得正前下方目标C的俯角为75°，这时飞机与地面目标的水平距离为（　　）

• A． 2500（$\sqrt{3}-1$）米
• B． 5000$\sqrt{2}$米
• C． 4000米
• D． 4000$\sqrt{2}$米

Answer 1

分析 在△ABC中，使用正弦定理求出BC，则飞机与地面目标的水平距离为BCcos75°．

解答 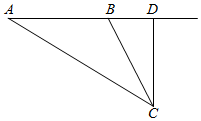解：过C作CD⊥AB交AB的延长线于D，由题意得A=30°，∠CBD=75°，AB=10000m，
∴∠ABC=105°，∠ACB=180°-A-∠ABC=45°，
在△ABC中，由正弦定理得$\frac{AB}{sin∠ACB}=\frac{BC}{sinA}$，即$\frac{10000}{\frac{\sqrt{2}}{2}}=\frac{BC}{\frac{1}{2}}$，
解得BC=5000$\sqrt{2}$．
∴BD=BC•cos∠CBD=5000$\sqrt{2}×$cos75°=5000$\sqrt{2}$×$\frac{\sqrt{6}-\sqrt{2}}{4}$=2500（$\sqrt{3}-1$）．
故选：A．

点评 本题考查了解三角形的实际应用，属于中档题．