Question

10．（1）若a是从0，1，2，3，4五个数中任取的一个数，b是从0，1，2中任取的一个数，求a与b的和为偶数的概率．
（2）若a是从[0，4]任取的一个实数，b是从[0，2]中任取的一个实数，求“a≥b”的概率．

Answer 1

分析 （1）确定基本事件的个数，即可求出概率；
（2）根据所给的条件作出试验发生是包含的所有事件是一个矩形区域，做出面积，看出满足条件的事件对应的面积，根据几何概型公式得到结果．

解答 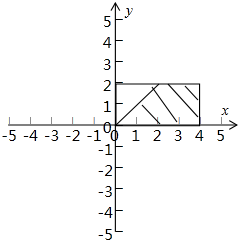解：（1）试验的结果共有5×3=15个，a与b的和的结果有2×1+3×2=8个，
∴a与b的和为偶数的概率为$\frac{8}{15}$．
（2）如图所示，矩形的面积S=8，
满足“a≥b”的事件如图阴影部分，面积为8-$\frac{1}{2}×2×2$=6，
∴所求概率为$\frac{6}{8}$=$\frac{3}{4}$．

点评 古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积的比值得到．