
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据回归方程的定义和性质分别进行判断即可.
解答 解:由线性回归方程为$\stackrel{∧}{y}$=7.19x+73.93可得直线的斜率k=7.19>0,则y与x具有正的线性相关关系,故①正确,
∵$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,$\overline{y}$=$\frac{1}{7}$(94.8+104.2+108.7+117.8+124.3+130.8+139.1)=117.1,即样本中心为(6,117.1),故②错误;
当x=10时,$\stackrel{∧}{y}$=7.19×10+73.93=145.83cm,即儿子10岁时的身高大约是145.83cm,不一定一定是145.83cm,故③错误,
儿子年龄增加1周岁,身高约增加7.19cm,故④正确,
故正确的是①④,
故选:B
点评 本题主要考查命题的真假判断,涉及线性回归方程的性质,难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
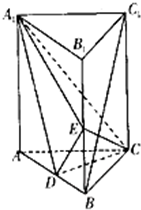 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.设AA1=AC=CB=2,AB=2$\sqrt{2}$,
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.设AA1=AC=CB=2,AB=2$\sqrt{2}$,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com