
| A. | [5,25] | B. | [1,25] | C. | $[{\frac{1}{2},20}]$ | D. | $[{\frac{5}{2},20}]$ |
分析 画出约束条件的可行域,利用目标函数的几何意义求解即可.
解答 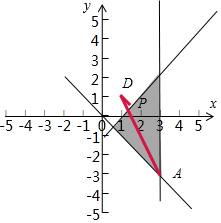 解:x,y满足$\left\{\begin{array}{l}x-y-1≥0\\ x+y≥0\\ x≤3\end{array}\right.$的可行域如图:
解:x,y满足$\left\{\begin{array}{l}x-y-1≥0\\ x+y≥0\\ x≤3\end{array}\right.$的可行域如图:
(x-1)2+(y-1)2的几何意义是可行域内的点与D(1,1)的距离的平方,
由图形可知DP距离的平方最小,DA距离的平方最大.
由$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$,解得A(3,-3).
(x-1)2+(y-1)2的最小值为:$(\frac{1}{\sqrt{2}})^{2}$=$\frac{1}{2}$.
(x-1)2+(y-1)2的最大值为:(3-1)2+(-3-1)2=20.
(x-1)2+(y-1)2的取值范围是[$\frac{1}{2}$,20]
故选:C.
点评 本题考查线性规划的简单应用,确定目标函数的几何意义是解题的关键,考查数形结合以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α2<β2 | B. | α2>β2 | C. | α<β | D. | α>β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-4≤x≤-2} | B. | {x|-1≤x≤3} | C. | {x|3<x≤4} | D. | {x|3≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 2017年5月14日“一带一路”国际合作高峰论坛在北京举行,会议期间,达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头.如图,工程师为了解深水港码头海域海底的构造,在海平面内一条直线上取A,B,C三点进行测量,已知AB=60cm,BC=120cm,在A处测得水深AD=120cm,在B处测得水深BE=200m,在C处测得水深CF=150m,则cos∠DEF=$-\frac{16}{65}$.
2017年5月14日“一带一路”国际合作高峰论坛在北京举行,会议期间,达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头.如图,工程师为了解深水港码头海域海底的构造,在海平面内一条直线上取A,B,C三点进行测量,已知AB=60cm,BC=120cm,在A处测得水深AD=120cm,在B处测得水深BE=200m,在C处测得水深CF=150m,则cos∠DEF=$-\frac{16}{65}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com