解:(Ⅰ)∵f(x)=ax
3+bx
2+cx(a≠0)是定义R上的奇函数
∴f(-x)=-f(x)恒成立,即bx
2=0对于x∈R恒成立,
∴b=0
∴f(x)=ax
3+cx,∴f′(x)=3ax
2+c
∵x=-1时,函数f(x)取极值1.
∴f′(-1)=0且f(-1)=1.
∴
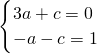
,
∴a=

,c=-

.
∴
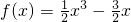
(Ⅱ)不等式f(x
1)-g(x
2)≤0恒成立,只需f(x)
max-g(x)
min≤0即可.
∵函数g(x)在[0,m]上单调递减,∴g(x)
min=g(m)=-m
2+

m
又
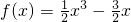
,
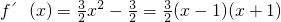
,
由f′(x)>0得x<-1或x>1;f′(x)<0得-1<x<1,
故函数f(x)在(-∞,-1),(1,+∞)上单调递增,在(-1,1)上单调递减,
则当x=1时,f(x)取得极小值,
在(0,+∞)上,当
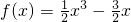
=f(0)时,x=

,
①当0<m≤

时,f(x)
max=f(0)=0,
则f(x)
max-g(x)
min=0-(-m
2+

m)=m
2-

m≤0,
解得
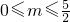
,故此时0<m≤

②当m>

时,f(x)
max=f(m)=
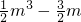
,
则f(x)
max-g(x)
min=
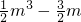
-(-m
2+

m)=

≤0,
解得-4≤m≤2,故此时

.
综上所述,实数m的取值范围是(0,2];
(Ⅲ)假定存在A(x
1,y
1),B(x
2,y
2)两点,
∵
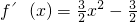
,过A、B两点的切线平行,∴f′(x
1)=f′(x
2),得

=

∵x
1≠x
2,∴x
2=-x
1,则y
2=-y
1,且知x
1≠0,
∴
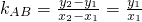
=
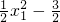
,
由于过A点的切线垂直于直线AB,∴(

)(
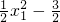
)=-1
∴3
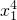
-12

+13=0,则△=-12<0,∴关于x
1的方程无解.
故曲线上不存在两个不同的点A、B,使过A、B两点的切线都垂直于直线AB.
分析:(Ⅰ)欲求f(x)的解析式,只需找到关于a,b,c的三个等式,求出a,b,c的值,根据函数的奇偶性可得到一个含等式,根据x=-1时,取得极值1,可知函数在x=-1时,导数等于0,且x=-1时,函数值等于1,又可得到两个含a,b,c的等式,三个等式联立,解出a,b,c即可;
(Ⅱ)不等式f(x
1)-g(x
2)≤0恒成立,只需f(x)
max-g(x)
min≤0即可;
(Ⅲ)先假设存在两个不同的点A、B,使过A、B的切线都垂直于AB,则切线斜率与AB斜率互为负倒数,又因为函数在A,B点处的切线斜率时函数在该点处的导数,就可得到含A,B点的坐标的方程,解方程,若方程有解,则假设成立,若方程无解,则假设不成立.
点评:本题考查函数的解析式,考查函数导数与函数切线斜率之间的关系,考查恒成立问题,属于中档题.

 m,若x1,x2∈[0.m](m>0),不等式f(x1)-g(x2)≤0恒成立,求m的取值范围;
m,若x1,x2∈[0.m](m>0),不等式f(x1)-g(x2)≤0恒成立,求m的取值范围;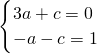 ,
, ,c=-
,c=- .
.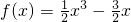
 m
m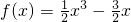 ,
,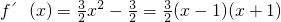 ,
,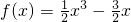 =f(0)时,x=
=f(0)时,x= ,
, 时,f(x)max=f(0)=0,
时,f(x)max=f(0)=0, m)=m2-
m)=m2- m≤0,
m≤0,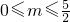 ,故此时0<m≤
,故此时0<m≤
 时,f(x)max=f(m)=
时,f(x)max=f(m)=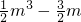 ,
,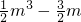 -(-m2+
-(-m2+ m)=
m)= ≤0,
≤0, .
.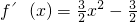 ,过A、B两点的切线平行,∴f′(x1)=f′(x2),得
,过A、B两点的切线平行,∴f′(x1)=f′(x2),得 =
=
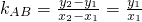 =
=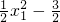 ,
, )(
)(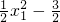 )=-1
)=-1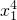 -12
-12 +13=0,则△=-12<0,∴关于x1的方程无解.
+13=0,则△=-12<0,∴关于x1的方程无解.
