
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据充分条件和必要条件的定义结合椭圆的方程进行判断即可.
解答 解:若足$\frac{{x}^{2}}{2+m}-\frac{{y}^{2}}{m+1}=1$表示椭圆,
则等价为$\frac{{x}^{2}}{m+2}$+$\frac{{y}^{2}}{-m-1}$=1,
则$\left\{\begin{array}{l}{m+2>0}\\{-m-1>0}\\{m+2≠-m-1}\end{array}\right.$即$\left\{\begin{array}{l}{m>-2}\\{m<-1}\\{m≠-\frac{3}{2}}\end{array}\right.$,
即-2<m<-1且m≠-$\frac{3}{2}$,
则p是q的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据椭圆的方程求出m的等价条件是解决本题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
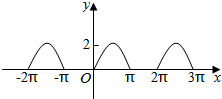
| A. | y=sinx-|sinx| | B. | y=|sinx|+sinx | C. | y=|sinx| | D. | y=|sinx|-sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com