
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn=n(3﹣bn),求数列{cn}的前n项和为Tn .
【答案】
(1)解:因为n=1时,a1+S1=a1+a1=2,所以a1=1.
因为Sn=2﹣an,即an+Sn=2,所以an+1+Sn+1=2.
两式相减:an+1﹣an+Sn+1﹣Sn=0,即an+1﹣an+an+1=0,故有2an+1=an.
因为an≠0,所以 ![]() =
= ![]() ( n∈N*).
( n∈N*).
所以数列{an}是首项a1=1,公比为 ![]() 的等比数列,an=
的等比数列,an= ![]() ( n∈N*)
( n∈N*)
(2)解:因为bn+1=bn+an( n=1,2,3,…),所以bn+1﹣bn= ![]() .从而有b2﹣b1=1,b3﹣b2=
.从而有b2﹣b1=1,b3﹣b2= ![]() ,b4﹣b3=
,b4﹣b3= ![]() ,…,bn﹣bn﹣1=
,…,bn﹣bn﹣1= ![]() ( n=2,3,…).
( n=2,3,…).
将这n﹣1个等式相加,得bn﹣b1=1+ ![]() +
+ ![]() +…+
+…+ ![]() =
=  =2﹣
=2﹣ ![]() .
.
又因为b1=1,所以bn=3﹣ ![]() ( n=1,2,3,…)
( n=1,2,3,…)
(3)解:因为cn=n (3﹣bn)= ![]() ,
,
所以Tn= ![]() . ①
. ①
![]() =
= ![]() . ②
. ②
①﹣②,得 ![]() =
= ![]() span> ﹣
span> ﹣ ![]() .
.
故Tn=  ﹣
﹣ ![]() =8﹣
=8﹣ ![]() ﹣
﹣ ![]() =8﹣
=8﹣ ![]() ( n=1,2,3,…)
( n=1,2,3,…)
【解析】(1)利用数列中an与 Sn关系 ![]() 解决.(2)结合(1)所求得出bn+1﹣bn=
解决.(2)结合(1)所求得出bn+1﹣bn= ![]() .利用累加法求bn(3)由上求出cn=n (3﹣bn)=
.利用累加法求bn(3)由上求出cn=n (3﹣bn)= ![]() ,利用错位相消法求和即可.
,利用错位相消法求和即可.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 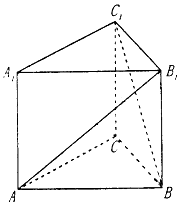
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),满足f(1)=0,且在(0,+∞)上单调递增,则xf(x)>0的解集为( )
A.{x|x<﹣1或x>1}
B.{x|0<x<1或﹣1<x<0}
C.{x|0<x<1或x<﹣1}
D.{x|﹣1<x<0或x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(a>0且a≠1)的图象经过点(2, ![]() ).
).
(1)比较f(2)与f(b2+2)的大小;
(2)求函数g(x)=a ![]() (x≥0)的值域.
(x≥0)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中真命题的序号为 .
①在空间中,m、n是两条不重合的直线,α、β是两个不重合的平面,如果α⊥β,α∩β=n,m⊥n,那么m⊥β;
②相关系数r的绝对值越接近于1,两个随机变量的线性相关性越强;
③用秦九昭算法求多项式f(x)=208+9x2+6x4+x6在x=﹣4时,v2的值为22;
④过抛物线y2=4x的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和等于4的直线有且只有两条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题: 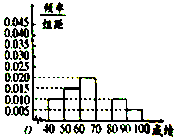
(1)求成绩在区间[70,80)内的频率,并补全这个频率分布直方图,并估计这次考试的及格率(60分及以上为及格);
(2)从成绩在[80,100]内的学生中选出三人,记在90分以上(含90分)的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 上有一个动点
上有一个动点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,动点
轴,动点![]() 在
在![]() 上,且满足
上,且满足![]() (
(![]() 为坐标原点),记点
为坐标原点),记点![]() 的轨迹为
的轨迹为![]() .
.
(I)求曲线![]() 的方程;
的方程;
(II)若直线![]() 是曲线
是曲线![]() 的一条切线,当点
的一条切线,当点![]() 到直线
到直线![]() 的距离最短时,求直线
的距离最短时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用网络外卖 | 偶尔或不用网络外卖 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com