
分析 (1)利用动圆与x轴相切,且与圆x2+y2-2y=0相外切,建立方程,即可求动圆圆心轨迹C的方程式.
(2)求出过M,N的直线方程为:$\frac{1}{2}ax-y-b=0$,又MN⊥OP,所以kMN•kOP=-1,$\frac{1}{2}a•\frac{b}{a}=-1$,所以b=-2,即可证明结论.
解答 解:(1)设动圆圆心C(x,y),(y>0),
因为动圆与x轴相切,且与圆x2+y2-2y=0相外切,所以$\sqrt{{x^2}+{{({y-1})}^2}}-1=|y|$,
又y>0,化简得:x2=4y,(y>0).┉┉┉┉┉┉┉┉(6分)
(2)设P(a,b)(a≠0,b≠0),由方程x2=4y,(y>0)得$y=\frac{1}{4}{x^2}$,两边对x求导得$y'=\frac{1}{2}x$.
设切点M(x1,y1),N(x2,y2)则M点处切线方程为$y-{y_1}=\frac{x_1}{2}({x-{x_1}})$.
又${y_1}=\frac{1}{4}{x_1}^2$,整理得:$\frac{1}{2}{x_1}x-y-{y_1}=0$,
又切线过P(a,b),所以$\frac{1}{2}{x_1}a-b-{y_1}=0$.
同理可得:$\frac{1}{2}{x_2}a-b-{y_2}=0$┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉(9分)
所以过M,N的直线方程为:$\frac{1}{2}ax-y-b=0$
又MN⊥OP,所以kMN•kOP=-1,$\frac{1}{2}a•\frac{b}{a}=-1$,所以b=-2.┉┉┉┉┉┉┉┉┉┉(11分)
直线MN:$\frac{1}{2}ax-y+2=0$过y轴上的定点(0,2).┉┉┉┉┉┉┉(12分)
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查导数知识的运用,知识综合性强.


科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
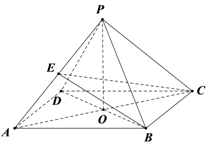 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com