
分析 本题考查的知识点是数学归纳法,由归纳法的性质,由P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立,结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立,由此不难得到答案.
解答 解:由题意可知,原命题成立则逆否命题成立,
P(n)对n=10时该命题不成立,(否则n=11也成立).
同理可推得P(n)对n=2,n=1也不成立.所以③正确
故答案为:③
点评 当P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立;结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | k≤1 | B. | 1≤k≤2 | C. | k≥1 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
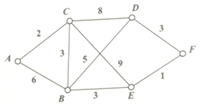 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com