
分析 由f(x)=(2x-3)ex+$\frac{a}{x}$=0,可得a=x(3-2x)ex,令y=x(3-2x)ex,则y′=-(x-1)(2x+3)ex,取得函数的单调性,求出函数的极值,即可得出结论.
解答 解:由f(x)=(2x-3)ex+$\frac{a}{x}$=0,可得a=x(3-2x)ex,(x≠0)
令y=x(3-2x)ex,则y′=-(x-1)(2x+3)ex,
∴x<-$\frac{3}{2}$或x>1时,y′<0,函数单调递减,-$\frac{3}{2}$<x<0或0<x<1时,y′>0,函数单调递增,
∴x=-$\frac{3}{2}$时,函数取得极小值-9${e}^{-\frac{3}{2}}$,x=1时,函数取得极大值e,
∵f(x)=(2x-3)ex+$\frac{a}{x}$有三个零点,当x趋于负无穷的时候y是趋于零的
∴-9${e}^{-\frac{3}{2}}$<a<0,
故答案为-9${e}^{-\frac{3}{2}}$<a<0.
点评 本题考查函数的零点,考查导数知识的运用,考查学生分析解决问题的能力,正确分离变量是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:解答题
已知数列 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)数列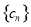 满足
满足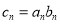 ,求数列
,求数列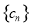 的前
的前 项和
项和
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com