考点:数列的求和
专题:证明题,导数的综合应用,点列、递归数列与数学归纳法
分析:(1)易求f′
n(x)=x
n-1(1-x)[n(1-x)-2x],经分析可得n=1时,
a1=f1()=;当
x∈[,)时f′
n(x)>0,当
x∈(,1)时f′
n(x)<0,函数f
n(x)在
x=处取得最大值,从而可得数列{a
n}的通项公式;
(2)当n≥2时,利用分析法:要证
an=≤,即证
(1+)n≥4,再利用二项式定理即可证得该式成立,从而使结论得证;
(3)当n=1,2时结论成立;当n≥3时,结合(2)的证明及放缩法的应用,即可证得对任意正整数n都有S
n<
成立.
解答:
解:(1)由
f′n(x)=nxn-1(1-x)2-2xn(1-x)=xn-1(1-x)[n(1-x)-2x],
当
x∈[,1]时,由f′(x)=0得x=1或
x=;
当n=1时,
=∉[,1],f′
1(x)=0,则
a1=f1()=;
当n=2时,
∈[,1],则
a2=f2()=;
当n≥3时,
∈[,1],
而当
x∈[,)时f′
n(x)>0,当
x∈(,1)时f′
n(x)<0,
故函数f
n(x)在
x=处取得最大值,
即:
an=fn()=,
综上:
an=…(6分)
(2)当n≥2时,要证
an=≤,即证
(1+)n≥4,
而
(1+)n=+•()1+•()2+…≥1+2+•≥4,
故不等式成立…(10分)
(3)当n=1,2时结论成立;
当n≥3时,由(2)的证明可知:
Sn=++a3+a4+…+an<++++…+<++(-)+(-)+…+(-)<++=,
从而
Sn<…(13分)
点评:本题考查数列的求和,考查数列通项公式的确定,突出考查导数的应用,考查分析法、放缩法的综合应用及推理论证能力,属于难题.



 阅读快车系列答案
阅读快车系列答案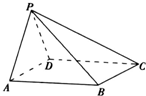 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.