
【题目】已知集合A是函数y=lg(6+5x﹣x2)的定义域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集.p:x∈A,q:x∈B.
(1)若A∩B=,求a的取值范围;
(2)若¬p是q的充分不必要条件,求a的取值范围.
【答案】
(1)解:由条件得:A={x|﹣1<x<6},B={x|x≥1+a或x≤1﹣a},
若A∩B=φ,则必须满足 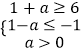 ,
,
所以,a的取值范围的取值范围为:a≥5
(2)解:易得:p:x≥6或x≤﹣1,
∵p是q的充分不必要条件,
∴{x|x≥6或x≤﹣1}是B={x|x≥1+a或x≤1﹣a}的真子集,
则 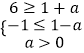 ,
,
∴a的取值范围的取值范围为:0<a≤2
【解析】(1)分别求函数y=lg(6+5x﹣x2)的定义域和不等式x2﹣2x+1﹣a2≥0(a>0)的解集化简集合A,由A∩B=得到区间端点值之间的关系,解不等式组得到a的取值范围;(2)求出p对应的x的取值范围,由p是q的充分不必要条件得到对应集合之间的关系,由区间端点值的关系列不等式组求解a的范围.
【考点精析】通过灵活运用集合的交集运算,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立即可以解答此题.
B,反之也成立即可以解答此题.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为O、P,与直线
与圆C的交点为O、P,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:4x2﹣y2=4及直线l:y=kx﹣1
(1)求双曲线C的渐近线方程及离心率;
(2)直线l与双曲线C左右两支各有一个公共点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Sn表示等差数列{an}的前n项的和,且S4=S9 , a1=﹣12
(1)求数列的通项an及Sn;
(2)求和Tn=|a1|+|a2|+…+|an|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题: 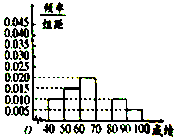
(1)求成绩在区间[70,80)内的频率,并补全这个频率分布直方图,并估计这次考试的及格率(60分及以上为及格);
(2)从成绩在[80,100]内的学生中选出三人,记在90分以上(含90分)的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log ![]()
![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)当x∈(1,+∞)时,f(x)+log ![]() (x+1)<m恒成立,求实数m的取值范围;
(x+1)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=log ![]() (x+k)在[2,3]上有解,求k的取值范围.
(x+k)在[2,3]上有解,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(4)班有男生28人,女生21人,用分层抽样的方法从全班学生中抽取一个调查小组,调查该校学生对2013年1月1日起执行的新交规的知晓情况,已知某男生被抽中的概率为 ![]() ,则抽取的女生人数为 .
,则抽取的女生人数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com