
| A. | y=x+$\frac{1}{x}$ | B. | y=x2+$\frac{1}{x^2}$ | C. | y=lgx+$\frac{1}{lgx}$ | D. | y=sinx+$\frac{1}{sinx}$ | ||||
| E. | y=x2+$\frac{1}{x^2}$ |
分析 利用基本不等式的性质.
解答 解:由基本不等式的性质$a+b≥2\sqrt{ab}$(a>0,b>0)
y=$x+\frac{1}{x}$,当x>0时,y≥2,当x<0时,y≤-2,∴A不对;
lgx+$\frac{1}{lgx}$中,当lgx>0时,y≥2,当lgx<0时,y≤-2,∴C不对;
同理,sinx+$\frac{1}{sinx}$中,当sinx>0时,y≥2,sinx<0时,y≤-2,∴D不对;
y=x2+$\frac{1}{x^2}$,∵${x}^{2}>0,\frac{1}{{x}^{2}}>0$,∴${x}^{2}+\frac{1}{{x}^{2}}≥2\sqrt{1}$成立,∴B对.
故选B.
点评 本题考查了基本不等式性质的利用,注意基本不等式的性质$a+b≥2\sqrt{ab}$中的a>0,b>0.如果无法确定,需要分正,负考虑.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
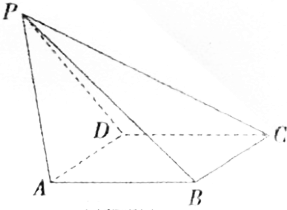 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{128}$,$\frac{1}{2}$) | B. | [$\frac{1}{64}$,$\frac{1}{2}$) | C. | [$\frac{1}{32}$,$\frac{1}{2}$) | D. | [$\frac{1}{16}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com