
分析 根据题意,由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标,计算可得$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,又由$({\overrightarrow a+\overrightarrow b})∥({\overrightarrow a-\overrightarrow b})$,则有(1+t)×(-2)=(1-t)×0=0,即可得t的值,即可得答案.
解答 解:根据题意,$\overrightarrow a=({1,-1}),\overrightarrow b=({t,1})$,
则$\overrightarrow{a}$+$\overrightarrow{b}$=(1+t,0),$\overrightarrow{a}$-$\overrightarrow{b}$=(1-t,-2),
若$({\overrightarrow a+\overrightarrow b})∥({\overrightarrow a-\overrightarrow b})$,则有(1+t)×(-2)=(1-t)×0=0,
解可得t=-1;
故答案为:-1.
点评 本题考查平面向量的坐标运算,关键是掌握向量平行的坐标表示方法.


科目:高中数学 来源: 题型:选择题
 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 2,4 | B. | 2,5 | C. | 0,4 | D. | 0,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
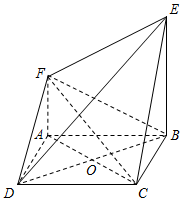 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )| A. | $\frac{\sqrt{3}}{2}π$ | B. | 4$\sqrt{3}$π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 8$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com