
分析 (Ⅰ)利用正弦定理化简asinA+csinC-$\sqrt{2}$asinC=bsinB,利用余弦定理即可求出角B的大小;
(Ⅱ)根据同角的三角函数关系,利用三角形内角和与两角和的正弦公式即可求出sinC.
解答 解:(Ⅰ)△ABC中,asinA+csinC-$\sqrt{2}$asinC=bsinB,
由正弦定理得a2+c2-$\sqrt{2}$ac=b2,
由余弦定理得
cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=$\frac{\sqrt{2}ac}{2ac}$=$\frac{\sqrt{2}}{2}$;
又B∈(0,π),
∴B=$\frac{π}{4}$;
(Ⅱ)由cosA=$\frac{1}{3}$,且A∈(0,π),
∴sinA=$\sqrt{1{-cos}^{2}A}$=$\frac{2\sqrt{2}}{3}$,
∴sinC=sin(A+B)
=sinAcosB+cosAsinB
=$\frac{2\sqrt{2}}{3}$×$\frac{\sqrt{2}}{2}$+$\frac{1}{3}$×$\frac{\sqrt{2}}{2}$
=$\frac{4+\sqrt{2}}{6}$.
点评 本题考查了正弦、余弦定理以及同角的三角函数关系,三角形内角和与两角和的正弦公式应用问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
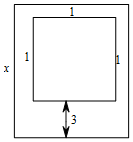 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥1 | B. | k>1 | C. | 0<k<1 | D. | 0<k≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+g(x)为偶函数 | B. | f(x)g(x)为奇函数 | C. | xf(x)-xg(x)为偶函数 | D. | f(|x|)+xg(x)为奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则a>c | B. | 若ac>bc,则a>b | ||
| C. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b | D. | 若a>b,c>d,则ac>bd |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com