
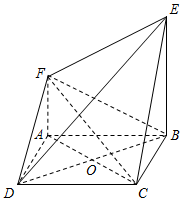
 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.分析 (I)取DE的中点G,连结OG,FG,通过证明四边形OAFG是平行四边形得出AO∥FG,从而得出AC∥平面DEF;
(II)通过证明AC⊥平面BDE得FG⊥平面BDE,从而得出平面BDE⊥平面DEF;
(III)作BH⊥DE,垂足为H,连结FH,则∠BFH为是直线BF与平面DEF所成的角,利用勾股定理计算BF,BD,DE得出BH,从而可得sin∠BFH.
解答 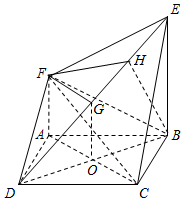 证明:(Ⅰ)连接AC,BD交点为O,取DE的中点G,连结OG,FG,
证明:(Ⅰ)连接AC,BD交点为O,取DE的中点G,连结OG,FG,
∵四边形ABCD为正形,∴O为BD中点.
∴OG∥BE,且OG=$\frac{1}{2}$BE.
又∵AF∥BE,AF=$\frac{1}{2}$BE,
∴AF∥OG,AF=OG,
∴四边形OAFG为平行四边形,
∴AO∥FG,即AC∥FG.
又AC?平面DEF,FG?平面DEF,
∴AC∥平面DEF.
(Ⅱ)∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AB⊥BE,
∴BE⊥平面ABCD.
∵AC?平面ABCD,∴BE⊥AC.
又四边形ABCD为正方形,∴AC⊥BD.
又BD∩BE=B,BD?平面BDE,BE?平面BDE,
∴AC⊥平面BDE.
由(Ⅰ)可知AC∥FG,∴FG⊥平面BDE,
又FG?平面DEF,
∴平面BDE⊥平面DEF,
(Ⅲ)作BH⊥DE,垂足为H,连结FH,
∵平面BDE⊥平面DEF,平面BDE∩平面DEF=DE,
∴BH⊥平面DEF.
∴∠BFH为是直线BF与平面DEF所成的角.
∵四边形ABCD是正方形,AB=BE=2,AF=1,
∴BD=2$\sqrt{2}$,DE=$\sqrt{B{E}^{2}+B{D}^{2}}$=2$\sqrt{3}$,BF=$\sqrt{A{F}^{2}+A{B}^{2}}$=$\sqrt{5}$,
∴BH=$\frac{BE•BD}{DE}$=$\frac{4\sqrt{2}}{2\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$,
∴sin∠BFH=$\frac{BH}{BF}$=$\frac{2\sqrt{30}}{15}$,
∴直线BF和平面DEF所成角的正弦值为$\frac{2\sqrt{30}}{15}$.
点评 本题考查了线面平行的判定,面面垂直的判定,线面角的计算,熟练掌握各位置关系的判定定理是证明的依据,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
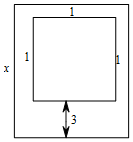 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com