
分析 (1)利用等差数列的求和公式,求商铺租出x年后的租金总和y;
(2)由0.2x2+5.2x≥72,可得结论;
(3)P(x)=(-0.3x2+10.56x+57.6+0.2x2+5.2x-72)÷x=-(0.1x+$\frac{14.4}{x}$)+15.76≤-2.4+15.76=13.36,即可得出结论.
解答 解:(1)第一年租金为5.4万元,以后每年租金比上一年增加0.4万元,
∴商铺租出x年后的租金总和y=5.4x+$\frac{x(x-1)}{2}×0.4$=0.2x2+5.2x(0<x≤40);
(2)由0.2x2+5.2x≥72,可得x≥10,即出租10年能收回成本;
(3)P(x)=(-0.3x2+10.56x+57.6+0.2x2+5.2x-72)÷x=-(0.1x+$\frac{14.4}{x}$)+15.76≤-2.4+15.76=13.36,
当且仅当0.1x=$\frac{14.4}{x}$,即x=12年,转让商铺,能使小A投资此商铺所得年平均收益P(x)最大.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
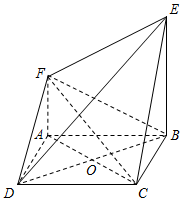 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )| A. | $\frac{\sqrt{3}}{2}π$ | B. | 4$\sqrt{3}$π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 8$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com