
分析 (Ⅰ)由椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{2}=1(a>\sqrt{2})$的离心率为$\frac{{\sqrt{2}}}{2}$,求出a=2,由此能求出椭圆的标准方程.
(Ⅱ)设M(x1,y1),N(x2,y2),则由$\overrightarrow{OP}$=$\overrightarrow{OM}+2\overrightarrow{ON}$,得x0=x1+2x2,y0=y1+2y2,由点M,N在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上,由直线OM与ON的斜率之积为-$\frac{1}{2}$,由此能求出存在常数λ=5,使得P点在椭圆$\frac{x^2}{4}+\frac{y^2}{2}=5$上.
解答 解:(Ⅰ)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{2}=1(a>\sqrt{2})$的离心率为$\frac{{\sqrt{2}}}{2}$,
∴e=$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,解得${b^2}={a^2}-{c^2}=\frac{a^2}{2}$,
又b2=2,解得a=2,
故椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1.(4分)
(Ⅱ)设M(x1,y1),N(x2,y2),则由$\overrightarrow{OP}$=$\overrightarrow{OM}+2\overrightarrow{ON}$,
得x0=x1+2x2,y0=y1+2y2,(6分)
又点M,N在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上,∴${{x}_{1}}^{2}+2{{y}_{1}}^{2}=4$,${{x}_{2}}^{2}+2{{y}_{2}}^{2}=4$,
设kOM,kON分别为直线OM,ON的斜率,由题意知:
kOM•kON=$\frac{{y}_{1}{y}_{2}}{{x}_{2}{x}_{2}}$=-$\frac{1}{2}$,∴x1x2+2y1y2=0,(8分)
∴$\frac{x_0^2}{4}+\frac{y_0^2}{2}=\frac{x_0^2+2y_0^2}{4}=\frac{{{{({x_1}+2{x_2})}^2}+2{{({y_1}+2{y_2})}^2}}}{4}$
=$\frac{{(x_1^2+2y_1^2)+4(x_2^2+2y_2^2)+4({x_1}•{x_2}+2{y_1}•{y_2})}}{4}=\frac{20}{4}=5$,(11分)
因此,存在常数λ=5,使得P点在椭圆$\frac{x^2}{4}+\frac{y^2}{2}=5$上.(12分)
点评 本题考查椭圆方程的求法,考查满足点在椭圆上的常数是否存在的判断与求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 2,4 | B. | 2,5 | C. | 0,4 | D. | 0,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
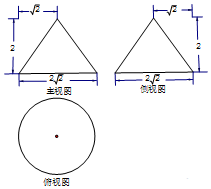 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $2-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
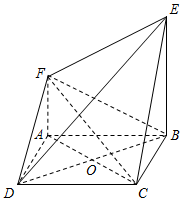 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com