
分析 通过函数在[-1,1]上有一个解或两个解,通过二次函数的性质以及零点定理解决.
解答 解:∵a>0,
∴当f(x)在[-1,1]上有一个零点时,$\left\{\begin{array}{l}{△=4+8a(3+a)=0}\\{-1≤\frac{1}{2a}≤1}\end{array}\right.$或f(-1)•f(1)≤0
解得1≤a≤5(6分);
当f(x)在[-1,1]上有两个零点时,则$\left\{\begin{array}{l}{a>0}\\{△=4+8a(3+a)>0}\\{-1<-\frac{1}{2a}<1}\\{f(-1)>0}\\{f(1)>0}\end{array}\right.$,解得a>5,
故实数a的取值范围为:[1,+∞)(12分).
点评 本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
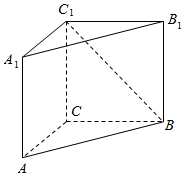 三棱柱ABC-A1B1C1的侧棱垂直底面,AC⊥BC,AC=BC=4,AA1=4.
三棱柱ABC-A1B1C1的侧棱垂直底面,AC⊥BC,AC=BC=4,AA1=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 终边在x轴负半轴上的角是零角 | B. | 第二象限角一定是钝角 | ||
| C. | 第四象限角一定是负角 | D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1-($\frac{5}{6}$)5]100 | B. | [1-($\frac{5}{6}$)100]5 | C. | 1-[1-($\frac{1}{6}$)100]5 | D. | 1-[1-($\frac{1}{6}$)5]100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com