
分析 (1)利用配方法,结合x=$\frac{1}{4}$时,f(x)有最小值-1,建立方程组,即可求a与b的值;
(2)f(x)<0即(log2x)2+4log2x+3<0,即可求出x的范围.
解答 解:(1)f(x)=(log2x)2-2alog2x+b=${{(log}_{2}^{x}-a)}^{2}$+b-a2(x>0),
当x=$\frac{1}{4}$时,f(x)有最小值-1,
∴$\left\{\begin{array}{l}{{log}_{2}^{\frac{1}{4}}=a}\\{b{-a}^{2}=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-2}\\{b=3}\end{array}\right.$;
(2)由(1)得:f(x)=(log2x)2+4log2x+3,
f(x)<0即(log2x+3)(log2x+1)<0,
解得:$\frac{1}{8}$<x<$\frac{1}{2}$.
点评 本题考查函数的最值,考查学生解不等式的能力,确定函数的解析式是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\int_{-π}^π$sinxdx=0 | B. | $\int_0^1$${\sqrt{x}$dx=$\frac{2}{3}}$ | ||
| C. | $\int_{-\frac{π}{2}}^{\frac{π}{2}}$cosxdx=2$\int_0^{\frac{π}{2}}$cosxdx | D. | $\int_{-1}^1$x2dx=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰三角或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2n | B. | (-2)n | C. | -4n | D. | (-4)n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
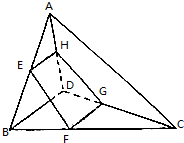 已知空间四边形ABCD,E、H分别是AB、AD的点,F、G分别是边BC、DC的点(如图),且EFGH是矩形,求证:
已知空间四边形ABCD,E、H分别是AB、AD的点,F、G分别是边BC、DC的点(如图),且EFGH是矩形,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com