Question

已知函数f（x）=ax²+4x+b（a＜0，且a，b∈R）．设关于x的不等式f（x）＞0的解集为（x₁，x₂），且方程f（x）=x的两实根为α，β．
（1）若|α-β|=1，求a，b的关系式；
（2）若α＜1＜β＜2，求证：（x₁+1）（x₂+1）＜7．

Answer 1

分析：（1）要求a，b的关系式，可根据方程f（x）=x的两实根为α，β．结合韦达定理（根与系数的关系），用a，b表示α，β．又则|α-β|=1，给出a，b的关系，但在分析过程中，要注意方程有两个不相等的根时，方程的判别式大于零．
（2）由α＜1＜β＜2，我们可以根据零点的存在定理，我们可以得到f（1），f（2）异号，代入可以构造一个关于a，b的不等式组，画出他们表示的平面区域，利用线性规划不难得到结论．

解答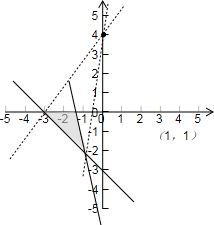：解：（1）由f（x）=x，
得ax²+3x+b=0，
由已知得9-4ab＞0，
∴α+β=-

3

a

，αβ=+

b

a

∴|α-β|=

(α+β)2-4αβ

=1，
∴

9

a2

-

4b

a

=1．
∴a²+4ab=9，
∴a、b的关系式为a²+4ab=9．
（2）令g（x）=ax²+3x+b，
又a＜0，α＜1＜β＜2．
∴

g(1)＞0 g(2)＜0

，
即

g(1)=a+b+3＞0 g(2)=4a+b+6＜0

又x₁，x₂是方程ax²+4x+b=0的两根，
∴x1+x2=-

4

a

，x1x2=

b

a

．
∴（x₁+1）（x₂+1）=x₁x₂+（x₁+x₂）+1=

b

a

-

4

a

+1=

b-4

a

+1
由线性约束条件

a+b+3＞0 4a+b+6＜0 a＜0.

，画图可知．

b-4

a

的取值范围为（-4，6），
∴-3＜

b-4

a

+1＜6+1=7．
∴（x₁+1）（x₂+1）＜7．

点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．