
| A. | ②③ | B. | ①③ | C. | ②④ | D. | ①②③ |
分析 将函数$f(x)=\frac{sinπx}{{({{x^2}+1})({{x^2}-2x+2})}}$=$\frac{sinπx}{{(x}^{2}+1)((x-1)^{2}+1})$,对以下各选项一次判断即可.
解答 解:由函数$f(x)=\frac{sinπx}{{({{x^2}+1})({{x^2}-2x+2})}}$=$\frac{sinπx}{{(x}^{2}+1)((x-1)^{2}+1})$
对于①函数f(x)显然不是周期函数.
对于②,因为sinπx有最值,函数f(x)的分母恒大于0,故f(x)有最大值又有最小值;②正确.
对于③,分母恒大于0,函数f(x)的定义域为R,sinπx是周期函数,其图象有对称轴,③正确.
对于④,f(-$\frac{1}{2}$)=-$\frac{16}{13}$,f(-$\frac{1}{3}$)=-$\frac{81\sqrt{3}}{500}$,∴f(-$\frac{1}{2}$)<f(-$\frac{1}{3}$),故④不正确,
故选A.
点评 本题考查命题的真假判断,考查三角函数知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
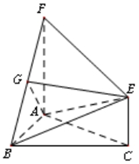 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
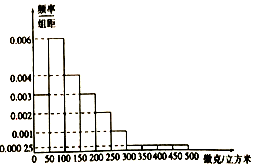 根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com