
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
分析 求出数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,数列{bn}的通项为bn=3n+2,从而得到cn=6n-1,由此能求出满足cm<2012的m的最大整数值.
解答 解:∵数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,
数列{bn}的前n项和为${S_n}=\frac{{3{n^2}+7n}}{2}({n∈{N^*}})$,
∴${b}_{1}={S}_{1}=\frac{3+7}{2}$=5,
bn=Sn-Sn-1=3n+2,
n=1时,上式成立,∴bn=3n+2,
∵这两个数列的公共项顺次构成一个新数列{cn},
∴{cn}中的项分别为5,11,17,23,…,
∴cn=5+(n-1)×6=6n-1,
∵cm<2012,
∴cm=6m-1<2012,解得m<335$\frac{1}{2}$,
c335=6×335-1=2009,c336=6×336-1=2015,
∴满足cm<2012的m的最大整数值为335.
故选:A.
点评 本题考查满足条件的最大整数的求法,考查等差数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
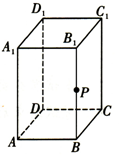 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2017×22016 | B. | 2017×22014 | C. | 2016×22017 | D. | 2016×22018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①③ | C. | ②④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com