
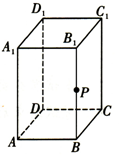
 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.分析 (1)由图可知,BC为三棱锥C-PAA1的高,且三角形PAA1的面积为定值,代入棱锥体积公式得答案;
(2)由剪展问题求出A1P+PC取得最小值时的P的位置,然后证明PD1⊥PA,PD1⊥PC,再由线面垂直的判定可得PD1⊥平面PAC.
解答 (1)解:在长方体中,BC⊥平面ABB1A1,∴C到平面PAA1的距离为BC=1,
又${S_{△PA{A_1}}}=\frac{1}{2}\;•\;A{A_1}\;•\;AB=\frac{1}{2}×2×1=1$,
∴${V_{C-PA{A_1}}}=\frac{1}{3}{S_{△PA{A_1}}}\;•\;BC=\frac{1}{3}×1×1=\frac{1}{3}$;
(2)证明:如图,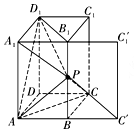
将侧面BCC1B1绕BB1展开至与平面ABB1A1共面,当A1,P,C′共线时,A1P+PC′取得最小值.
∵在△A1AC′中,为AC′中点,BP∥AA1,∴P为BB1的中点.
如图,连接PA,PC,AC,PD1,AD1,B1D1,
在Rt△PAB中,求得$PA=\sqrt{2}$,
在Rt△ADD1中,求得$A{D_1}=\sqrt{5}$,
∵PB1⊥平面A1B1C1D1,∴PB1⊥B1D1,
在Rt△PB1D1中,PB1=1,${B_1}{D_1}=\sqrt{2}$,得$P{D_1}=\sqrt{3}$,
∵在△APD1中,$A{D_1}^2=P{A^2}+P{D_1}^2$,∴PD1⊥PA.
同理可得PD1⊥PC,又PC∩PA=P,
∴PD1⊥平面PAC.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,考查多面体体积的求法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年降水量(mm) | [200,250] | [250,300] | [300,350] | [350,400] |
| 概率 | 0.30 | 0.21 | 0.14 | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
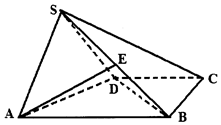 已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.
已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com