
分析 (Ⅰ)求出函数的导数,通过y=-2x+b为f(x)的一条切线,利用斜率,求解b值.
(Ⅱ)求出函数的极值点,列表推出导函数的符号,然后函数的极值,转化求解实数m的取值范围.
解答 解:(Ⅰ)函数f(x)=-x3+x-1,f′(x)=-3x2+1,
设切点为(x0,y0).故-3x02+1=-2,∴x0=±1所以切点为(1,-1),(-1,-1),
代入y=-2x+b,得b=1或-3.…(4分)
(Ⅱ)令g(t)=f(t)-(-2t+m)=-t3+3t-1-m,
由g′(t)=-3t2+3=0得t=1,t=-1(不合题意,舍去).
当t变化时g′(t),g(t)的变化情况如下表:
| t | (0,1) | 1 | (1,2) |
| g′(t) | + | 0 | - |
| g(t) | 递增 | 极大值1-m | 递减 |
点评 本题考查函数的导数的应用,切线方程以及函数的最值的求法,考查转化思想以及计算能力.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
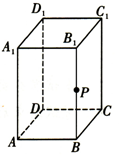 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
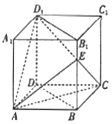 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}i$ | D. | $\frac{3}{4}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com