
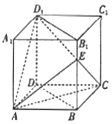
 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1分析 (1)由底面ABCD为菱形,可得AC⊥BD,再由已知可得BB1⊥AC,利用线面垂直的判定可得AC⊥平面BDD1B1,进一步得到平面ACE丄平面BDD1B1;
(2)连接BC1,过E作EF∥BC1 交B1C1于F,则B1F=1,可得平面AED1 与侧面BCC1B1相交的线段为EF,故平面AED1 将四棱柱ACCD-A1B1C1D1分成上下两部分.由棱台体积求得上部分是三棱台B1EF-A1AD1 的体积,再由四棱柱ABCD-A1B1C1D1的体积减去上部分的体积得到下部分的体积,则两部分的休积之比可求.
解答 (1)证明:∵底面ABCD为菱形,∴AC⊥BD,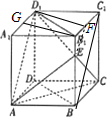
在直四棱柱ACCD-A1B1C1D1中,∵BB1⊥底面ABCD,∴BB1⊥AC,
∵BB1∩BD=B,∴AC⊥平面BDD1B1,
又AC?平面ACE,∴平面ACE丄平面BDD1B1;
(2)解:连接BC1,过E作EF∥BC1 交B1C1于F,则B1F=1,
则平面AED1 与侧面BCC1B1相交的线段为EF,
故平面AED1 将四棱柱ACCD-A1B1C1D1分成上下两部分.
上部分是三棱台B1EF-A1AD1,取A1D1 的中点G,连接B1G,
∵底面ABCD为菱形,∠BAD=60°,
∴△ABD为正三角形,即△A1B1D1也为正三角形,
∴B1G⊥A1D1,又AA1⊥底面A1B1C1D1,
∴AA1⊥B1G,而A1D1∩A1A=A1,
∴B1G⊥平面AA1D1,
∵${S}_{△{B}_{1}EF}=\frac{1}{2}$,${S}_{△{A}_{1}A{D}_{1}}=8$,${B}_{1}G=2\sqrt{3}$,
∴${V}_{{B}_{1}EF-{A}_{1}A{D}_{1}}={V}_{上}=\frac{1}{3}×(\frac{1}{2}+2+8)×2\sqrt{3}$=$7\sqrt{3}$.
又四棱柱ABCD-A1B1C1D1的体积为$32\sqrt{3}$,
∴${V}_{下}=32\sqrt{3}-{V}_{上}=25\sqrt{3}$.
∴$\frac{{V}_{上}}{{V}_{下}}=\frac{7}{25}$.
点评 本题考查平面与平面垂直的判定,考查了空间想象能力和思维能力,训练了多面体体积的求法,是中档题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{26}}}{13}$ | B. | $\frac{{\sqrt{26}}}{26}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [0,1] | C. | $[{0,\frac{e}{2}}]$ | D. | [0,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com