
分析 (1)根据三角函数在周期公式和性质可得函数f(x)的最小正周期和最大值.
(2)将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;即可求解在[-2π,2π]上的单调增区间.
解答 解:函数$f(x)=sin(\frac{1}{2}x+\frac{π}{3})$
(1)函数f(x)的最小正周期T=$\frac{2π}{\frac{1}{2}}=4π$,
根据正弦三角函数的图象和性质:当$\frac{1}{2}x+\frac{π}{3}=\frac{π}{2}+2kπ$时,
即x=$4kπ+\frac{π}{3}$,函数f(x)取得最大值为1.
可得f(x)取得最大值时x的集合为{x|x=$4kπ+\frac{π}{3}$,k∈Z}
(2)令$-\frac{π}{2}+2kπ≤\frac{1}{2}x+\frac{π}{3}≤\frac{π}{2}+2kπ$,
得$-\frac{5π}{3}+4kπ≤x≤\frac{π}{3}+4kπ,k∈Z$,
设A=[-2π,2π]
$B=[-\frac{5π}{3}+4kπ,\frac{π}{3}+4kπ]k∈Z$
所以,$A∩B=[-\frac{5π}{3},\frac{π}{3}]$
即函数f(x)在[-2π,2π]上的单调增区间为$[-\frac{5π}{3},\frac{π}{3}]$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用.属于基础题.


科目:高中数学 来源: 题型:解答题
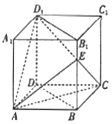 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”.
为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”.| 空间想象能力突出 | 空间想象能力正常 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(X2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
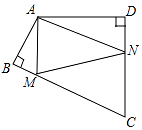 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>ef(0),f(2016)>e2016f(0) | B. | f(1)<ef(0),f(2016)>e2016f(0) | ||
| C. | f(1)>ef(0),f(2016)<e2016f(0) | D. | f(1)<ef(0),f(2016)>e2016f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com