Question

14．设函数$f（x）=\frac{1}{2}{x^3}-a{x^2}+1$．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）方程f（x）=0有三个不同的解，求a的范围．

Answer 1

分析 （Ⅰ）求出函数f（x）的导数，求出极值点，利用电话的符号，判断函数的单调性求解函数的单调区间；
（Ⅱ）利用函数的极值，列出不等式求解即可．

解答 解：（Ⅰ）函数$f（x）=\frac{1}{2}{x^3}-a{x^2}+1$．
$f'（x）=\frac{3}{2}{x^2}-a$，
令f'（x）=0，得$\frac{3}{2}{x^2}-a=0$，${x^2}=\frac{2}{3}a$，
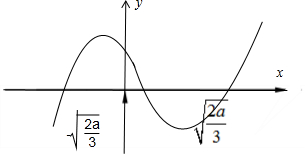
①当a＞0时，$x=-\sqrt{\frac{2a}{3}}$或$x=\sqrt{\frac{2a}{3}}$．

x	$（-∞，-\sqrt{\frac{2a}{3}}）$	$-\sqrt{\frac{2a}{3}}$	$（-\sqrt{\frac{2a}{3}}，\sqrt{\frac{2a}{3}}）$	$\sqrt{\frac{2a}{3}}$	$（\sqrt{\frac{2a}{3}}，+∞）$
f'（x）	+	0	-	0	+
f（x）	增函数	极大值	减函数	极小值	增函数

当$x∈（-∞，-\sqrt{\frac{2a}{3}}]$及$x∈[\sqrt{\frac{2a}{3}}，+∞）$时，f（x）单调递增；
当$x∈[-\sqrt{\frac{2a}{3}}，\sqrt{\frac{2a}{3}}]$时，f（x）单调递减．
②当a≤0时，有f'（x）≥0，
此时，当x∈（-∞，+∞）时，f（x）单调递增．
（Ⅱ）由题意知，当a＞0时f（x）示意图如下
：
即$\left\{{\begin{array}{l}{f（-\sqrt{\frac{2a}{3}}）＞0}\\{f（\sqrt{\frac{2a}{3}}）＜0}\end{array}}\right.$，
于是$\left\{{\begin{array}{l}{\frac{1}{2}{{（-\sqrt{\frac{2a}{3}}）}^3}-a（-\sqrt{\frac{2a}{3}}）+1＞0}\\{\frac{1}{2}{{（\sqrt{\frac{2a}{3}}）}^3}-a（\sqrt{\frac{2a}{3}}）+1＜0}\end{array}}\right.$，
即$\left\{{\begin{array}{l}{a＞0}\\{a＞\frac{3}{2}}\end{array}}\right.$，得$a＞\frac{3}{2}$．
故$a∈（\frac{3}{2}，+∞）$．

点评 本题考查函数的导数的应用，函数的单调性以及函数的极值的求法，考查分析问题解决问题的能力．