
分析 (Ⅰ)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)根据f(x)的单调性求出f(x)在[a,b]的值域,令$F(x)=\frac{f(x)}{x+2}=\frac{{{x^2}-xlnx+2}}{x+2}(x≥\frac{1}{2})$,根据函数的单调性求出k的范围即可.
解答 解:(Ⅰ)令g(x)=f'(x)=2x-lnx-1(x>0),
令g′(x)>0,解得:x>$\frac{1}{2}$,令g′(x)<0,解得:0<x<$\frac{1}{2}$,
所以g(x)在$(0,\frac{1}{2})$单调递减,在$(\frac{1}{2},+∞)$单调递增,
则g(x)的最小值为$g(\frac{1}{2})=ln2>0$.
所以$f'(x)=g(x)≥g(\frac{1}{2})>0$,
所以f(x)的单调递增区间为(0,+∞)
(Ⅱ)由(Ⅰ)得f(x)在区间$[a,b]⊆[\frac{1}{2},+∞)$递增,
∵f(x)在[a,b]上的值域是[k(a+2),k(b+2)]
所以$f(a)=k(a+2),f(b)=k(b+2),\frac{1}{2}≤a<b$.
则f(x)=k(x+2)在$[\frac{1}{2},+∞)$上至少有两个不同的正根,
$k=\frac{f(x)}{x+2}$,令$F(x)=\frac{f(x)}{x+2}=\frac{{{x^2}-xlnx+2}}{x+2}(x≥\frac{1}{2})$
求导,得$F'(x)=\frac{{{x^2}+3x-2lnx-4}}{{{{(x+2)}^2}}}(x≥\frac{1}{2})$,
令$G(x)={x^2}+3x-2lnx-4(x≥\frac{1}{2})$
则$G'(x)=2x+3-\frac{2}{x}=\frac{(2x-1)(x+2)}{x}≥0$.
所以G(x)在$[\frac{1}{2},+∞)$递增,
$G(\frac{1}{2})<0,G(1)=0$.
当$x∈[\frac{1}{2},1)$时,G(x)<0∴F'(x)<0,
当x∈(1,+∞)时,G(x)>0∴F'(x)>0
所以F(x)在$[\frac{1}{2},1)$上递减,在(1,+∞)上递增,
故$F(1)<k≤F(\frac{1}{2})∴k∈(1,\frac{9+2ln2}{10}]$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2013×2015 | B. | 2014×2016 | C. | 2015×2017 | D. | 2016×2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2017×22016 | B. | 2017×22014 | C. | 2016×22017 | D. | 2016×22018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①③ | C. | ②④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
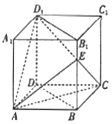 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com