
| A. | (-∞,1] | B. | [0,1] | C. | $[{0,\frac{e}{2}}]$ | D. | [0,e] |
分析 依题意,分a=0,a<0,a>0三类讨论,将不等式(ax+1)(ex-aex)≥0在(0,+∞)上恒成立转化为a≥-$\frac{1}{x}$在(0,+∞)上恒成立(a<0)或ex-aex≥0在(0,+∞)上恒成立(a>0),再分别构造函数,解之即可.
解答 解:∵不等式(ax+1)(ex-aex)≥0在(0,+∞)上恒成立,
∴①当a=0时,(ax+1)(ex-aex)=ex>0在(0,+∞)上恒成立;
②当a<0时,ex-aex>0恒成立,故不等式(ax+1)(ex-aex)≥0在(0,+∞)上恒成立
?ax+1≥0在(0,+∞)上恒成立?a≥-$\frac{1}{x}$在(0,+∞)上恒成立.
∵y=-$\frac{1}{x}$在(0,+∞)上单调递增,
∴当x→+∞时,y→0,
∴a≥0,又a<0,∴a∈∅;
③当a>0时,ax+1>0恒成立,故不等式(ax+1)(ex-aex)≥0在(0,+∞)上恒成立
?ex-aex≥0在(0,+∞)上恒成立?a≤$\frac{{e}^{x-1}}{x}$在(0,+∞)上恒成立,
因此,a≤($\frac{{e}^{x-1}}{x}$)min,
令g(x)=$\frac{{e}^{x-1}}{x}$(x>0),则g′(x)=$\frac{{xe}^{x-1}{-e}^{x-1}}{{x}^{2}}$=$\frac{{(x-1)e}^{x-1}}{{x}^{2}}$(x>0),
当0<x<1时,g′(x)<0,g(x)在区间(0,1)上单调递减;
当x>1时,g′(x)>0,g(x)在区间(1,+∞)上单调递增;
∴当x=1时,g(x)=$\frac{{e}^{x-1}}{x}$(x>0)取得极小值g(1)=1,也是最小值,
∴0<a≤1,
综上所述,0≤a≤1,
故选:B.
点评 本题考查函数恒成立问题,突出考查分类讨论思想与等价转化思想、函数与方程思想及导数的综合运用,对a分a=0,a<0,a>0三类讨论是关键,属于难题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:选择题

| A. | 2017×22016 | B. | 2017×22014 | C. | 2016×22017 | D. | 2016×22018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
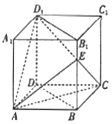 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}i$ | D. | $\frac{3}{4}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com