
分析 求出cosC=2cos2$\frac{C}{2}$-1=$\frac{1}{9}$,sinC=$\frac{4\sqrt{5}}{9}$,由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{9}$,从而ab$≤\frac{9}{4}$,由此能求出△ABC面积的最大值.
解答 解:∵在△ABC中,角A、B、C所对的边分别是a、b、c,cos$\frac{C}{2}$=$\frac{\sqrt{5}}{3}$,且c=2,
∴cosC=2cos2$\frac{C}{2}$-1=2×$\frac{5}{9}$-1=$\frac{1}{9}$,
∴sinC=$\sqrt{1-(\frac{1}{9})^{2}}$=$\frac{4\sqrt{5}}{9}$,
∵cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{9}$,∴ab$≤\frac{9}{4}$,
∴△ABC面积:
S=$\frac{1}{2}absinC$≤$\frac{1}{2}×\frac{9}{4}×\frac{4\sqrt{5}}{9}$=$\frac{\sqrt{5}}{2}$.
∴△ABC面积的最大值为$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查三角形面积的最大值的求法,考查余弦定理、三角形面积公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:选择题
已知复数 (
( ),则“
),则“ ”是“
”是“ 为纯虚数”的 ( )
为纯虚数”的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 既不充分也不必要条件 D. 充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [$\frac{1}{2}$,1) | C. | (0,$\frac{1}{2}$] | D. | ($\frac{1}{2},\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
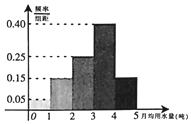 为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.
为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com