
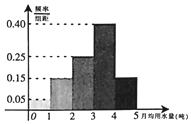
 Ϊ�˽�ij����������ˮ�����ͨ�������������100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��1����[1��2������[4��5]�ֳ�5�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
Ϊ�˽�ij����������ˮ�����ͨ�������������100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��1����[1��2������[4��5]�ֳ�5�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ�ܹ�����100λ�����¾���ˮ��������ƽ�������������
��2���¾���ˮ��С��2�ֵ�������ռƵ��Ϊ0.2��������Ƶ����Ϊ���ʣ��Ӹõ������������ࣩܶ����ѡ3�ˣ����¾���ˮ��С��2�ֵ�����Ϊ�������X����X��B��3��0.2�����ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ������100λ�����¾���ˮ��������ƽ������
x=0.5��0.05+1.5��0.15+2.5��0.25+3.5��0.4+4.5��0.15=2.95��3.0��
��������s2=��0.5-3��2��0.05+��1.5-3��2��0.15+��2.5-3��2��0.25+��3.5-3��2��0.4+��4.5-3��2��0.15��1.2��
��2���¾���ˮ��С��2�ֵ�������ռƵ��Ϊ0.2��
������Ƶ����Ϊ���ʣ��Ӹõ������������ࣩܶ����ѡ3�ˣ����¾���ˮ��С��2�ֵ�����Ϊ�������X��
��X��B��3��0.2����
P��X=0��=${C}_{3}^{0}0��{8}^{3}$=0.512��
P��X=1��=${C}_{3}^{1}��0.2��0��{8}^{2}$=0.384��
P��X=2��=${C}_{3}^{2}��0��{2}^{2}��0.8$=0.096��
P��X=3��=${C}_{3}^{3}��0��{2}^{3}$=0.008��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | 0.512 | 0.384 | 0.096 | 0.008 |
���� ���⿼��Ƶ�ʷ�ֱ��ͼ��Ӧ�ã�������ɢ����������ĸ��ʷֲ���ѧ�����������е��⣬����ʱҪ�������⣬ע�����ֲ������ʵĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017���������гǹ��ظ���10�µ�����ѧ�������Ծ��������棩 ���ͣ������
��֪Բ ��˫����
��˫���� �������������ཻ��
�������������ཻ�� ��
�� ��
�� ��
�� �ĵ㣬���ı���
�ĵ㣬���ı��� �����Ϊ
�����Ϊ ����
���� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2\sqrt{2}}{3}$ | B�� | $\frac{1}{3}$ | C�� | -$\frac{2\sqrt{2}}{3}$ | D�� | -$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 2 | C�� | -2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com