
【题目】对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是( )
A.﹣1是f(x)的零点
B.1是f(x)的极值点
C.3是f(x)的极值
D.点(2,8)在曲线y=f(x)上
【答案】A
【解析】解:可采取排除法. 若A错,则B,C,D正确.即有f(x)=ax2+bx+c的导数为f′(x)=2ax+b,
即有f′(1)=0,即2a+b=0,①又f(1)=3,即a+b+c=3②,
又f(2)=8,即4a+2b+c=8,③由①②③解得,a=5,b=﹣10,c=8.符合a为非零整数.
若B错,则A,C,D正确,则有a﹣b+c=0,且4a+2b+c=8,且 ![]() =3,解得a∈,不成立;
=3,解得a∈,不成立;
若C错,则A,B,D正确,则有a﹣b+c=0,且2a+b=0,且4a+2b+c=8,解得a=﹣ ![]() 不为非零整数,不成立;
不为非零整数,不成立;
若D错,则A,B,C正确,则有a﹣b+c=0,且2a+b=0,且 ![]() =3,解得a=﹣
=3,解得a=﹣ ![]() 不为非零整数,不成立.
不为非零整数,不成立.
故选:A.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】圆C过点A(6,4),B(1,﹣1),且圆心在直线l:x﹣5y+7=0上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD. (Ⅰ)证明:BM⊥平面SMC;
(Ⅱ)若SB与平面ABCD所成角为 ![]() ,N为棱SC上的动点,当二面角S﹣BM﹣N为
,N为棱SC上的动点,当二面角S﹣BM﹣N为 ![]() 时,求
时,求 ![]() 的值.
的值.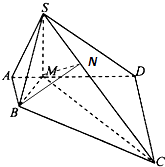
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,福建省大力推进海峡西岸经济区建设,福州作为省会城市,在发展过程中,交通状况一直倍受有关部门的关注,据有关统计数据显示上午6点到10点,车辆通过福州市区二环路某一路段的用时y(分钟)与车辆进入该路段的时刻t之间关系可近似地用如下函数给出:y= 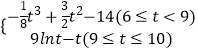 .求上午6点到10点,通过该路段用时最多的时刻.
.求上午6点到10点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+ ![]() (x>0).
(x>0).
(1)若y=g(x)﹣m有零点,求m的取值范围;
(2)确定m的取值范围,使得g(x)﹣f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+bx+c)ex在[0,1]上单调递减且满足f(0)=1,f(1)=0.
(1)求a取值范围;
(2)设g(x)=f(x)﹣f′(x),求g(x)在[0,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线过定点P(2,1).
(1)求经过点P且在两坐标轴上的截距相等的直线方程;
(2)若过点P的直线l与x轴和y轴的正半轴分别交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com