
【题目】已知a,b,c均大于1,且logaclogbc=4,则下列各式中,一定正确的是( )
A.ac≥b
B.ab≥c
C.bc≥a
D.ab≤c
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
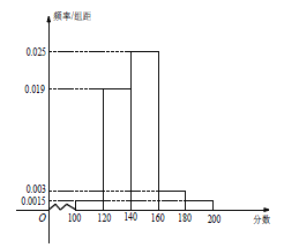
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.

(Ⅰ)求证:AC⊥FB
(Ⅱ)求二面角E﹣FB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是( )
A.﹣1是f(x)的零点
B.1是f(x)的极值点
C.3是f(x)的极值
D.点(2,8)在曲线y=f(x)上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右顶点与右焦点的距离为
右顶点与右焦点的距离为![]() ,短轴长为
,短轴长为![]()
(I)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为![]() 求直线AB的方程。
求直线AB的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m∈R,复数z=(m2﹣3m﹣4)+(m2+3m﹣28)i,其中i为虚数单位.
(1)当m为何值时,复数z是虚数?
(2)当m为何值时,复数z是纯虚数?
(3)当m为何值时,复数z所对应的点在复平面内位于第四象限?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 是
是![]() 的中点,底面
的中点,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,平面
,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() .
.
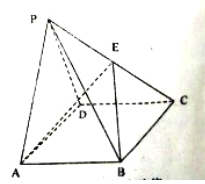
(1)求证: ![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com