
【题目】如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.

(Ⅰ)求证:AC⊥FB
(Ⅱ)求二面角E﹣FB﹣C的大小.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意结合线面垂直的判定定理可证得AC⊥平面FCB,据此有AC⊥FB.
(Ⅱ)建立空间直角坐标系,结合半平面的法向量可得二面角E﹣FB﹣C的大小为![]() .
.
试题解析:
(Ⅰ)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,
∴AD⊥平面CDEF,∴AD⊥FC,
∵四边形CDEF为正方形.∴DC⊥FC
由DC∩AD=D ∴FC⊥平面ABCD,∴FC⊥AC
又∵四边形ABCD为直角梯形,
AB∥CD,AD⊥DC,AD=2,AB=4
∴![]() ,
, ![]() ,则有AC2+BC2=AB2∴AC⊥BC
,则有AC2+BC2=AB2∴AC⊥BC
由BC∩FC=C,∴AC⊥平面FCB,∴AC⊥FB.
(Ⅱ)解:由(I)知AD,DC,DE所在直线相互垂直,故以D为原点,以![]() 的方向分别为x,y,z轴的正方向,建立如图所示的空间直角坐标系D-xyz…
的方向分别为x,y,z轴的正方向,建立如图所示的空间直角坐标系D-xyz…
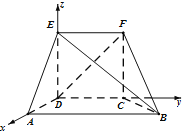
可得D(0,0,0),F(0,2,2),B(2,4,0),
E(0,0,2),C(0,2,0),A(2,0,0),
由(Ⅰ)知平面FCB的法向量为![]()
∵![]() ,
, ![]() …
…
设平面EFB的法向量为![]() 则有
则有![]() 即
即![]()
令![]() 则
则![]()
设二面角E﹣FB﹣C的大小为θ,有图易知![]() 为锐角
为锐角
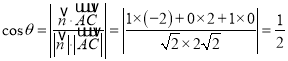
所以二面角E﹣FB﹣C的大小为![]() …
…


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球. (I)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD. (Ⅰ)证明:BM⊥平面SMC;
(Ⅱ)若SB与平面ABCD所成角为 ![]() ,N为棱SC上的动点,当二面角S﹣BM﹣N为
,N为棱SC上的动点,当二面角S﹣BM﹣N为 ![]() 时,求
时,求 ![]() 的值.
的值.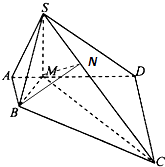
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+ ![]() (x>0).
(x>0).
(1)若y=g(x)﹣m有零点,求m的取值范围;
(2)确定m的取值范围,使得g(x)﹣f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() 为( )
为( )

A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com