练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列四个命题：
    ①三棱锥A1-D1DP的体积不变；  
    ②A1P∥平面ACD1；
    ③DP⊥BC1；  
    ④平面A1PB⊥平面PDB1．
    其中正确的命题的序号是（　　）
    A．①②③B．①②④C．①③④D．②③④

    分析 利用ABCD-A1B1C1D1为正方体，根据正方体的性质及线面平行、线面垂直、面面平行和垂直的判定和性质，逐一核对四个命题得答案．

    解答 解：如图，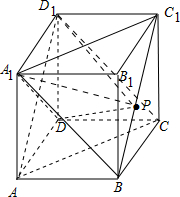

    对于①，∵BC1∥平面A1DD1，∴P到面A1DD1的距离不变，三棱锥A1-D1DP的体积不变，①正确；  
    对于②，∵平面A1BC1∥平面ACD1，∴A1P∥平面ACD1，②正确；
    对于③，∵在同一平面内，过直线外一点与已知直线垂直的直线只有一条，∴DP⊥BC1不正确，③不正确；  
    对于④，∵BD1⊥平面A1BC1，由线面垂直的判断知，平面A1PB⊥平面PDB1，④正确．
    故正确的命题为①②④．
    故选：B．

    点评 本题考查了命题的真假判断与应用，考查了空间先和面的位置关系，训练了系数的空间想象能力和思维能力，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．设x，y∈R且满足$\left\{\begin{array}{l}{x≥1}\\{x+y-6≤0}\\{y≥x}\end{array}\right.$，则z=x+2y的最小值等于（　　）
    A．2B．3C．9D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=cos（-$\frac{x}{2}$）+sin（$π-\frac{x}{2}$），x∈R
    （1）求函数f（x）的最小正周期与最大值
    （2）求函数f（x）在[0，π）上单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知P（B）＞0，A1A2=∅，则下列式子成立的是（　　）
    ①P（A1|B）＞0②P（A1∪A2|B）=P（A1|B）+P（A2|B）③P（A1$\overrightarrow{{A}_{2}}$|B）≠0④P（$\overline{{A}_{1}{A}_{2}}$|B）=1．
    A．①②③④B．②C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1，F2，点M在椭圆上，且MF1⊥F1F2，|MF1|=$\frac{4}{3}$，|MF2|=$\frac{14}{3}$，则离心率e等于（　　）
    A．$\frac{{\sqrt{5}}}{8}$B．$\frac{{\sqrt{5}}}{6}$C．$\frac{{\sqrt{5}}}{3}$D．$\frac{{\sqrt{5}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设f（x）是定义在R上且周期为2的函数，在区间[-1，1]上，f（x）=$\left\{\begin{array}{l}{ax+1，-1≤x＜0}\\{\frac{bx+2}{x+1}，0≤x≤1}\end{array}\right.$，其中a，b∈R，若f（$\frac{1}{2}$）=f（$\frac{3}{2}$），则3a+2b=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

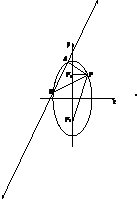    15．已知F1，F2是椭圆$\frac{y^2}{4}+\frac{x^2}{2}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，直线l：y=$\sqrt{2}$x+m与椭圆交于A，B两点．
    （1）求点P的坐标；
    （2）求△PAB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

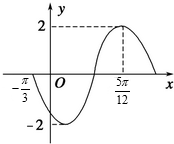
    16．函数f（x）=Acos（ωx+φ）（ A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则f（${\frac{5π}{6}}$）=-$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案