考点:利用导数研究函数的极值
专题:导数的综合应用
分析:f(x)得f′(x)=3x
2+6bx+3c由题意知方程f′(x)=0有两个根x
1,x
2,且x
1∈[-1,0],x
2∈[1,2]则由根的分布得有2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0,可得-2≤c≤0,用消元法消去参数b,利用参数c表示出f(x
1)和f(x
1)的值域,再利用参数c的范围能证明0
≤f(x1)≤,-10
≤f(x2)≤-.
解答:
证明:f′(x)=3x
2+6bx+3c,
由题意知方程f′(x)=0有两个根x
1,x
2,且x
1∈[-1,0],x
2∈[1,2],
则有f′(-1)≥0,f′(0)≤0,f′(1)≤0,f′(2)≥0.
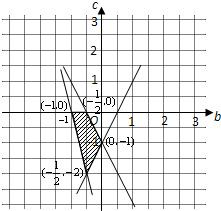
即满足下列条件2b-c-1≤0,c≤0,2b+c+1≤0且4b+c+4≥0
∴有图中四边形ABCD即是满足这些条件的点(b,c)的区域.
∴-2≤c≤0
由题设知f′(x
1)=3x
12+6bx
1+3c=0,
则bx
1=-
x
12-
c,
∴f(x
1)=-
x13+
x1,
由于x
1∈[-1,0],c≤0,
∴0≤f(x
1)≤
-
,
∵-2≤c≤0,
∴0≤f(x
1)≤
.
f′(x
2)=3x
22+6bx
2+3c=0,
bx
2=-
x
22-
c,
∴f(x
2)=-
x23+
x2,
由于x
2∈[1,2],c≤0,
∴-4+3c≤f(x
2)≤-
+c.
∵-2≤c≤0,
∴-10
≤f(x2)≤-.
点评:本题考查不等式的证明,解决此类问题的关键是熟悉导数与实根分布问题的处理方法,有难度.



