Question

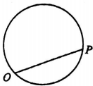
6．如图，点P从点O出发，按逆时针方向沿周长为l的圆周运动一周，则O，P两点连线的距离y与点P走过的路程x的函数图象可能是（　　）

• A．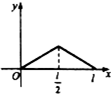
• B．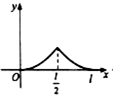
• C．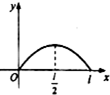
• D．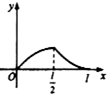

Answer 1

分析 首先根据题意求出圆的半径，进一步利用弦与所对的弧长之间的关系建立等量，求出结果，可得结论．

解答 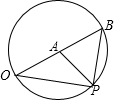解：已知圆的周长为l，则设圆的半径为r，则：l=2πr
所以：r=$\frac{l}{2π}$
设O，P两点连线的距离为y，点P走过的路程为x，连接AP，设∠OAP=θ，
则：x=$\frac{l}{2π}$θ
整理得：$\frac{θ}{2}=\frac{πx}{l}$
利用sin$\frac{θ}{2}$=$\frac{\frac{y}{2}}{\frac{l}{2π}}$=$\frac{πy}{l}$
则：y=$\frac{l}{π}sin（\frac{πx}{l}）$．
故选：C．

点评 本题考查的知识要点：弧长关系式的应用，及相关的运算问题，考查数形结合的数学思想，属于中档题．