
分析 用x,y表示出|PA|2+|PB|2,根据x,y的关系消去二次项,转化为线性规划解决问题.
解答 解:设P(x,y),则(x-3)2+(y-2)2=5,
∴x2+y2-6x-4y+8=0,
∴x2+y2=6x+4y-8.
∴|PA|2+|PB|2=(x-4)2+(y-10)2+(x-8)2+(y-6)2=2x2+2y2-24x-32y+216=-12x-24y+200,
令z=-12x-24y+200,则12x+24y+z-200=0,
∴当直线12x+24y+z-200=0与圆C相切时,z取得最大值和最小值.
此时圆C的圆心到直线的距离d=$\sqrt{5}$.
∴$\frac{|z-116|}{\sqrt{1{2}^{2}+2{4}^{2}}}$=$\sqrt{5}$,解得z=176或z=56.
∴|PA|2+|PB|2的最大值为176,最小值为56.
点评 本题考查了直线与圆的位置关系,简单的线性规划问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 23 | C. | 34 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
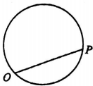 如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )
如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )| A. | 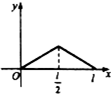 | B. | 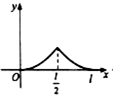 | C. | 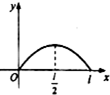 | D. | 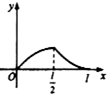 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
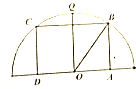 如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.
如图,四边形ABCD是半径为1的半圆O的内接矩形,其中A、D在直径上,Q为弧CB的中点,设∠BOQ=θ,记f(θ)=$\frac{1}{OA}$+$\frac{1}{AB}$,求f(θ)的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com