Question

11．设函数f（x）=xe^x-ax+a，若存在唯一的整数x₀，使得f（x₀）＜0，则实数a的取值范围是（　　）

• A． [-$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$）
• B． [$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$）
• C． [-$\frac{1}{{e}^{2}}$，$\frac{1}{e}$）
• D． [$\frac{1}{{e}^{2}}$，$\frac{1}{e}$）

Answer 1

分析 令y=xe^x，y=ax-a，从而讨论两个函数的性质作出y=xe^x与y=ax-a的图象，从而结合图象可知$\left\{\begin{array}{l}{f（0）=a≥0}\\{f（-1）=-\frac{1}{e}+2a＜0}\\{f（-2）=-2\frac{1}{{e}^{2}}+3a≥0}\end{array}\right.$或$\left\{\begin{array}{l}{f（1）=e＞0}\\{f（2）=2{e}^{2}-2a+a＜0}\\{f（3）=3{e}^{3}-3a+a≥0}\end{array}\right.$，从而解得．

解答 解：令y=xe^x，y=ax-a，
∵y′=e^x（x+1），
∴y=xe^x在（-∞，-1]上是减函数，在（-1，+∞）上是增函数，
又∵y=ax-a是恒过点（1，0）的直线，
∴作y=xe^x与y=ax-a的图象如下，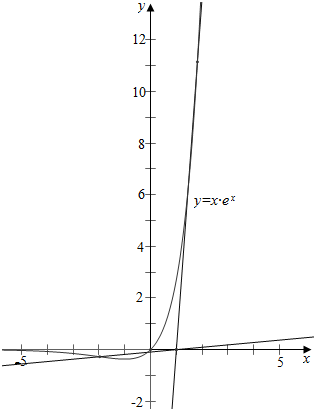
，
当直线y=ax-a与y=xe^x相切时，设切点为（x，xe^x），
则$\frac{x{e}^{x}}{x-1}$=e^x+xe^x，
则x=$\frac{1-\sqrt{5}}{2}$，x=$\frac{1+\sqrt{5}}{2}$；
结合图象可知，$\left\{\begin{array}{l}{f（0）=a≥0}\\{f（-1）=-\frac{1}{e}+2a＜0}\\{f（-2）=-2\frac{1}{{e}^{2}}+3a≥0}\end{array}\right.$或$\left\{\begin{array}{l}{f（1）=e＞0}\\{f（2）=2{e}^{2}-2a+a＜0}\\{f（3）=3{e}^{3}-3a+a≥0}\end{array}\right.$，
解得，a∈[$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$）∪（2e²，$\frac{3}{2}$e³]，
故选：B．

点评 本题考查了函数的零点与函数的图象的交点的关系应用及数形结合的思想应用．