考点:利用导数研究函数的单调性,函数恒成立问题
专题:导数的综合应用
分析:(1)令h(x)=ln(1+x)-
,得到h′(x)=
,从而求出h(x)在(0,+∞)上是增函数,故h(x)>h(0)=0,结论证出;
(2)不等式f(x)<
可化为:
<0,令g(x)=(1+x)ln(1+x)-x-kx
2,则g′(x)=ln(1+x)-2kx,从而g″(x)=
-2k,对x分情况进行讨论:①x>0时,②-1<x<0时,从而证出结论.
解答:
解:(1)令h(x)=ln(1+x)-
,
∴h′(x)=
,
x>0时,h′(x)>0,
∴h(x)在(0,+∞)上是增函数,
故h(x)>h(0)=0,
即:ln(1+x)>
.
从而,x>0时,f(x)>
得证.
(2)不等式f(x)<
可化为:
<0,
令g(x)=(1+x)ln(1+x)-x-kx
2,
则g′(x)=ln(1+x)-2kx
g″(x)=
-2k,
①x>0时,有0<
<1,
令2k≥1,则g″(x)<0,
故g′(x)在(0,+∞)上是减函数,即g′(x)<g′(0)=0,
∴g(x)在(0,+∞)上是减函数,
从而,g(x)<g(0)=0,
∴k≥
时,对于x>0,有
<0,
②-1<x<0时,有
>1,
令2k≤1,则g″(x)>0,
故g′(x)在(-1,0)上是增函数,即:g′(x)<g′(0)=0
∴g(x)在(-1,0)上是减函数.
从而,g(x)>g(0)=0.
∴当k≤
时,对于-1<x<0,有
<0.
综合①②,当k=
时,在x>-1且x≠0时,有f(x)<
.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,本题是一道中档题.



 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵. 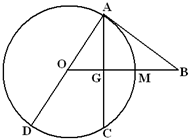 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.