
【题目】证明:任何一个正方形均可分割成![]() 个全等的非矩形图形,其中,
个全等的非矩形图形,其中,![]() 、
、![]() 为互不相等的素数.
为互不相等的素数.
【答案】见解析
【解析】
若存在一个矩形可分割成![]() 个全等的非矩形图形,则可通过倍长这个矩形的两边长将其拉伸成一个正方形.
个全等的非矩形图形,则可通过倍长这个矩形的两边长将其拉伸成一个正方形.
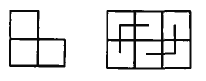
此时,可考虑用较简单的“角形”(如图4)来分割该矩形.
因此,只需说明存在![]() 个角形拼成的矩形,也就是说存在一个面积为
个角形拼成的矩形,也就是说存在一个面积为![]() 的矩形可完全分割成角形即可,不妨设
的矩形可完全分割成角形即可,不妨设![]() .
.
当![]() 时,对任意的素数
时,对任意的素数![]() ,必存在一个面积为
,必存在一个面积为![]() 的矩形可分割成角形(由
的矩形可分割成角形(由![]() 个
个![]() 的矩形并排组成的矩形),即任何一个正方形可分割成
的矩形并排组成的矩形),即任何一个正方形可分割成![]() 个全等的非矩形图形.
个全等的非矩形图形.
当![]() 时,只需说明存在一个面积为
时,只需说明存在一个面积为![]() 的矩形可分割成角形即可.
的矩形可分割成角形即可.
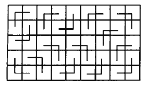
先将一个![]() 的矩形分割成15个角形(如图5),称该矩形为“基本矩形”.
的矩形分割成15个角形(如图5),称该矩形为“基本矩形”.
(1)若![]() ,
,![]() ,其基本矩形就是它的分割.故命题成立.
,其基本矩形就是它的分割.故命题成立.
若![]() ,
,![]() ,由
,由![]() 为素数,知
为素数,知![]() 为奇数.
为奇数.
此时,只需在基本矩形下添若干行![]() 的矩形即可,而每个
的矩形即可,而每个![]() 的矩形是由三个
的矩形是由三个![]() 的矩形并排而成,可分割成角形.故命题成立.
的矩形并排而成,可分割成角形.故命题成立.
(2)若![]() ,由(1),知可用角形拼成一个
,由(1),知可用角形拼成一个![]() 的矩形.
的矩形.
由于![]() ,又
,又![]() 为奇素数,
为奇素数,![]() 为
为![]() 的倍数,因此,可在原
的倍数,因此,可在原![]() 的矩形右侧添加若干个
的矩形右侧添加若干个![]() 的矩形,而每个
的矩形,而每个![]() 的矩形可分割成角形,它们一起构成一个面积为
的矩形可分割成角形,它们一起构成一个面积为![]() 的矩形.
的矩形.
故命题成立.
综上,对任意的素数![]() 、
、![]() ,均存在一个矩形,可将其分割成
,均存在一个矩形,可将其分割成![]() 个角形.
个角形.
从而,任何一个正方形均可分割成![]() 个全等的非矩形图形,其中,
个全等的非矩形图形,其中,![]() 、
、![]() 为互不相等的素数.
为互不相等的素数.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.

(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且
,且![]() 过点
过点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆,经过点
为直径的圆,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次飞机航程中,调查男女晕机情况,在80名男乘客中有10人晕机,70人不晕机.在30名女乘客中有10人晕机,20人不晕机
(1)请根据题设数据列出![]() 列联表
列联表
晕机 | 不晕机 | 总计 | |
男 | |||
女 | |||
总计 |
(2)是否有![]() 把握认为“是否晕机与性别有关”.
把握认为“是否晕机与性别有关”.
附:![]()
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点,
轴的交点,![]() 、
、![]() 分别是
分别是![]() 的图象上横坐标为
的图象上横坐标为![]() 、
、![]() 的两点,
的两点,![]() 轴,且
轴,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.

(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上恰好有一个零点,求实数
上恰好有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组: ![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:

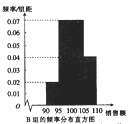
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期;
的分布列及数学期;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信”和“QQ”是腾讯社交体系中的两款产品,小明为了解不同群体对这两款产品的首选情况,统计了周围老师和同学关于首选“微信”或“QQ”的比例,得到如图等高条形图.根据等高条形图中的信息,可判断下列说法正确的是( )
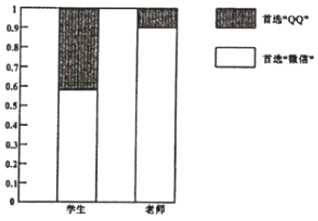
A.对老师而言,更倾向于首选“微信”
B.对学生而言,更倾向于首选“QQ”
C.首选“微信”的老师比首选“微信”的同学多
D.如果首选“微信”的老师比首选“微信”的同学多,则小明统计的老师人数一定比学生多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com