考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆E的方程.
(Ⅱ)点B(-2,0),C(2,0),设G(x,0),A(x,y),|GA|=
=
,由此能求出|GA|的取值范围.
(Ⅲ)设直线l
1:y=kx-1,直线l
2:x+ky+k=0,直线l
1被圆x
2+y
2=4所截的弦长|MN|=
,由
,得(k
2+1)x
2+8kx=0,|DP|=
=
,由此能求出△MND面积的最大值.
解答:
解:(Ⅰ)∵椭圆E:
+
=1(a>b>0)的离心率为
,其中一个焦点F(
,0),
∴
,解得a
2=4,b
2=1,
∴椭圆E的方程是
+y2=1.
(Ⅱ)∵点B(-2,0),C(2,0),
设G(x,0),根据题意得(2-x,0)=3(x+2,0),
设点A(x,y),则
+y2=1,
|GA|=
=
=
,
∵-2≤x≤2,
∴当x=-
时,|GA|有最小值
;当x=2时,|GA|有最大值3.
∴|GA|的取值范围是[
,3].
(Ⅲ)∵直线l
1⊥l
2,且都过点P(0,-1),
①当直线l
1,l
2的斜率都存在时,
设直线l
1:y=kx-1,直线l
2:x+ky+k=0,
∴圆心(0,0)到直线l
1:kx-y-1=0的距离为
d=,
∴直线l
1被圆x
2+y
2=4所截的弦长|MN|=2
=
,
由
,得(k
2+1)x
2+8kx=0,
∴
xD+xP=-,
∴|DP|=
=
,
S△MND=|MN||DP|=
××=
=
=
=
≤
.
当且仅法
=,即k
2=
时,等号成立,
∴△MND面积的最大值为
.
②当l
1,l
2有一条斜率不存在时,△MND的面积为
2,
综上所述,△MND面积的最大值为
.
点评:本题考查椭圆方程的求法,考查线段取值范围的求法,考查三角形面积的最大值的求法,解题时要认真审题,注意两点间距离公式的合理运用.

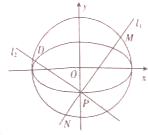 已知椭圆E:
已知椭圆E:

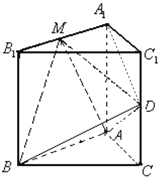 (文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(文)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=