
分析 (1)求出函数的导数,通过讨论a的范围确定导函数的符号,从而求出函数的单调区间;
(2)求出f(x)-f′(x)的表达式,分别令$g(x)=\frac{1}{2}({x-lnx}),h(x)=\frac{5}{2x}+\frac{1}{x^2}-\frac{2}{x^3}-\frac{1}{2},x∈[{1,2}]$,则f(x)-f′(x)=g(x)+h(x),根据函数的单调性怎么即可.
解答 解:(1)f(x)的定义域为(0,+∞),
${f^/}(x)=a({1-\frac{1}{x}})-\frac{2}{x^2}+\frac{2}{x^3}=\frac{{({a{x^2}-2})({x-1})}}{x^3}$,
当a≤0,x∈(0,1)时,f′(x)>0,f(x)单调递增,
x∈(1,+∞)时,f′(x)<0,f(x)单调递减,
当a>0时,f′(x)=$\frac{a(x-1)}{{x}^{3}}$(x+$\sqrt{\frac{2}{a}}$)(x-$\sqrt{\frac{2}{a}}$),
①0<a<2时$\sqrt{\frac{2}{a}}>1$,
当$x∈({0,1})或x∈({\sqrt{\frac{2}{a}},+∞})$时,f′(x)>0,f(x)单调递增,
当x∈(1,$\sqrt{\frac{2}{a}}$)时,f′(x)<0,f(x)单调递减;
②a=2时$\sqrt{\frac{2}{a}}=1$,当x∈(0,+∞)时f′(x)≥0,f(x)单调递增;
③a>2时,$0<\sqrt{\frac{2}{a}}<1$,
当$x∈({0,\sqrt{\frac{2}{a}}})或x∈({1,+∞})时,{f^/}(x)>0,f(x)$单调递增,
当$x∈({\sqrt{\frac{2}{a}},1})$时,f′(x)<0,f(x)单调递减;
综上所述,
当a≤0时,函数f(x)在(0,1)内单调递增,在(1,+∞)内单调递减;
当0<a<2时,函数f(x)在(0,1)内单调递增,在1,$\sqrt{\frac{2}{a}}$)内单调递减,在($\sqrt{\frac{2}{a}}$,+∞)内单调递增;
当a=2时,函数f(x)在(0,+∞)内单调递增;
当a>2时,函数f(x)在(0,$\sqrt{\frac{2}{a}}$)内单调递增,在($\sqrt{\frac{2}{a}}$,1)内单调递减,在(1,+∞)内单调递增.
(2)证明:由(1)知,$a=\frac{1}{2}$时,
$f(x)-{f^/}(x)=\frac{1}{2}({x-lnx})+\frac{2}{x}-\frac{1}{x^2}-\frac{1}{2}({1-\frac{1}{x}})+\frac{2}{x^2}-\frac{2}{x^3}$
=$\frac{1}{2}({x-lnx})+\frac{5}{2x}+\frac{1}{x^2}-\frac{2}{x^3}-\frac{1}{2},x∈[{1,2}]$,
设$g(x)=\frac{1}{2}({x-lnx}),h(x)=\frac{5}{2x}+\frac{1}{x^2}-\frac{2}{x^3}-\frac{1}{2},x∈[{1,2}]$,
f(x)-f′(x)=g(x)+h(x)则g′(x)=$\frac{x-1}{2x}$≥0,
∴$g(x)≥g(1)=\frac{1}{2}$,当且仅当x=1时取等号,
又${h^/}(x)=\frac{{-5{x^2}-4x+12}}{{2{x^4}}}$,设ϕ(x)=-5x2-4x+12,则ϕ(x)在x∈[1,2]单调递减,
∴?x0∈[1,2]使得x∈(1,x0)时ϕ(x)>0,x∈(x0,2)时ϕ(x)<0,
∴h(x)在(1,x0)上单调递增,在(x0,2)上单调递减,
∵$h(1)=1,h(2)=\frac{3}{4}∴h(x)≥h(2)=\frac{3}{4}当且仅当x=2时取得等号$,
∴$f(x)-{f^/}(x)>g(1)+h(2)=\frac{5}{4}$,
即$f(x)>{f^/}(x)+\frac{5}{4}$对于任意的x∈[1,2]成立.
点评 本题考查利用导函数判断函数的单调性;考查分类讨论思想和转化思想,是一道中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
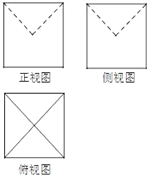 某几何体的三视图如图所示,图中的四边形都是边长为6的正方形,两条虚线互相垂直,则该几何体的体积是 ( )
某几何体的三视图如图所示,图中的四边形都是边长为6的正方形,两条虚线互相垂直,则该几何体的体积是 ( )| A. | 96 | B. | 108 | C. | 180 | D. | 198 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或0 | B. | 0 | C. | -2或2 | D. | -2或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2) | C. | {0,1} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com