练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．编号为1，2，3，4，5，6的六个人分别去坐编号为1，2，3，4，5，6的六个座位，其中有且只有两个人的编号与座位编号一致的坐法有（　　）
    A．135种B．90种C．150种D．15种

    分析 根据题意，首先从6个号码中，选出两个号码，使其编号与座位号一致，由组合数公式可得情况数目，再分析其余的四个座位与人的编号不同的情况数目，易得第一个人有3种坐法，第二有2种坐法，第三，四个人都有1种坐法；由分步计数原理相乘得到结果．

    解答 解：根据题意，先确定编号与座位号相同的两人，有C62=15种情况，
    剩下的四人编号与座位号都不一致，第一个人有3种坐法，第二有2种坐法，第三，四个人都有1种坐法，共有3×2×1×1=6种坐法，
    则一共有15×6=90种坐法；
    故选B．

    点评 本题考查组合公式以及分步计数原理的运用，易错点为当两个相同的号码确定以后，其余的四个号码不同的排的结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．过圆外一点P作圆的两条切线和一条割线，切点为A，B，所作割线交圆于C，D两点，C在P，D之间，在弦CD上取一点Q，使∠DAQ=∠PBC．求证：∠DBQ=∠PAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

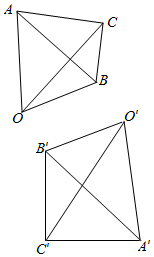    10．如图所示，有点O，O′和△A′B′C′，满足下列条件：$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，$\overrightarrow{O{{\;}^{'}A}^{'}}$=-$\overrightarrow{a}$，$\overrightarrow{O{{\;}^{'}B}^{'}}$=-$\overrightarrow{b}$，O′C′=-$\overrightarrow{c}$，求证：△ABC≌△A′B′C′．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．在?ABCD中，已知$\overrightarrow{AC}$=（-4，2），$\overrightarrow{BD}$=（2，-6），那么|2$\overrightarrow{AB}$+$\overrightarrow{AD}$|=（　　）
    A．5$\sqrt{5}$B．2$\sqrt{5}$C．2$\sqrt{10}$D．$\sqrt{85}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若α∈（0，$\frac{π}{3}$），则${5}^{{|log}_{5}（cosα）|}$=（　　）
    A．cosαB．$\frac{1}{cosα}$C．-cosαD．-$\frac{1}{cosα}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．等差数列{an}的通项公式是an=2n+1，其前n项和为Sn，求数列{$\frac{{S}_{n}}{n}$}的前10项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．函数y=5sin（$\frac{π}{4}$-2x）的单调递增区间是[kπ+$\frac{3π}{8}$，kπ+$\frac{7π}{8}$]，k∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）=3sin（$\frac{x}{4}$+$\frac{π}{6}$）（x∈R）的最小正周期（　　）
    A．2πB．4πC．8πD．π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如果ξ～B $（{20，\frac{1}{3}}）$，则使P（ξ=k）取最大值时的k值为（　　）
    A．5或6B．6或7C．7或8D．以上均错

    查看答案和解析>>

    同步练习册答案